student2023042 LV 3 @ 2024-12-15 15:08:19

![]1.说明要绘制的函数，以及定义域x的范围。绘制三角函数图像

2.截取绘制函数的图像。

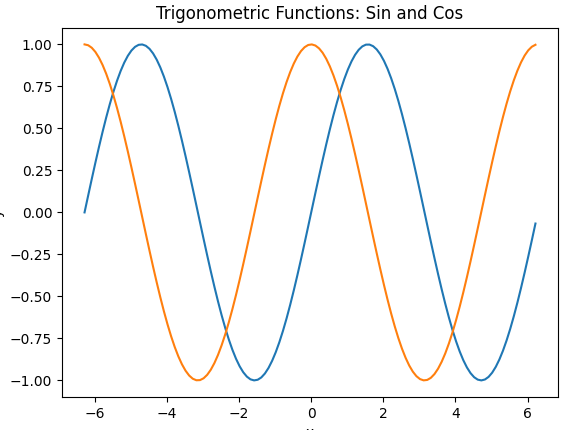
3.说明你对函数图像的观察与思考。

X轴呈左右变化，Y轴呈上下变化。函数y=f(x)与y=f(-x)的图像关于y 轴对称。函数y=f(x)与y=-f(c)的图像关于x 轴对称。

4.提供绘制函数图像的代码。

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-2 * np.pi, 2 * np.pi, 0.1)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, label='y = sin(x)')
plt.plot(x, y2, label='y = cos(x)')
plt.title('Trigonometric Functions: Sin and Cos')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

student2023047 LV 1 @ 2024-12-15 13:23:25

1.说明要绘制的函数，以及定义域x的范围 y = x ** 2，定义域 x 的范围设定在 [-5, 5] 2提供绘制函数图像的代码

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 100)
y = x ** 2
plt.plot(x, y)
plt.title("Function: y = x ** 2")
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show(

student2023014 LV 2 @ 2024-12-15 12:45:55

1.说明要绘制的函数，以及定义域x的范围基本指数函数 x = np.linspace(-10,10, 100) -10和10中取100个点 2.截取绘制函数的图像

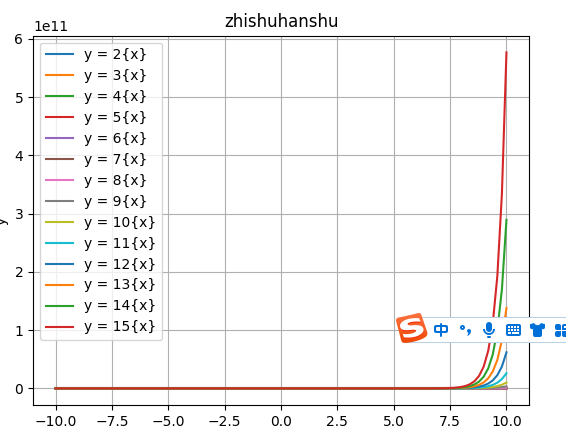3.说明你对函数图像的观察与思考。函数底数越大，增长率越大·



```import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10,10, 100)

a1 = [2,3,4,5,6,7,8,9,10,11,12,13,14,15]

for a in a1:
    y = a ** x
    plt.plot(x, y, label=f'y = {a}{{x}}')


plt.title("zhishuhanshu")

plt.xlabel('x')

plt.ylabel('y')

plt.legend()

plt.grid(True)
plt.show()

student2023029 LV 1 @ 2024-12-14 14:25:59

已修改

1.说明要绘制的函数，以及定义域x的范围

用plot和bar一副五彩斑斓的图画， x = np.linspace(-1, 1, 600) 从-1到1之间生成600个点

2.截取绘制函数的图像

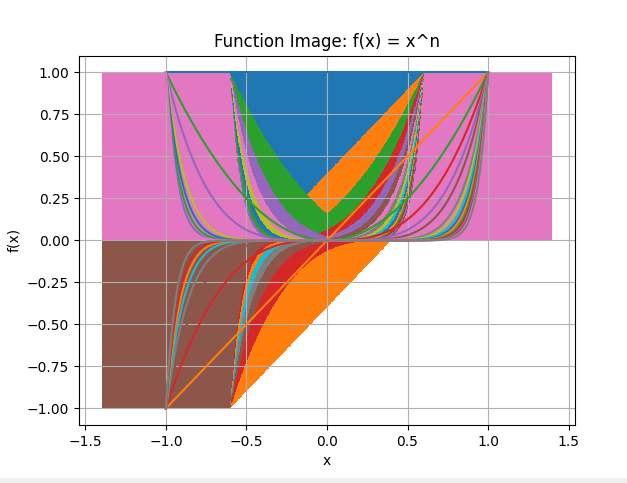
3.说明你对函数图像的观察与思考

限制的函数范围越大，形成的图像越单调和片面，而在点数相同的情况下，函数范围越小，越丰富，细节化和全面

4.提供绘制函数图像的代码

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-1, 1, 600)  # 从-10到10之间生成400个点
y = x**0
y1 = x**1
y2 = x**2
y3 = x**3
y4 = x**4
y5 = x**5
y6 = x**6
y7 = x**7
y8 = x**8
y9 = x**9
y10 = x**10
y11 = x**11
y12 = x**12
y13 = x**13
y14 = x**14
y15 = x**15
y16 = x**16
y17 = x**17
y18 = x**18




# 绘制图像
plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y4)
plt.plot(x, y5)
plt.plot(x, y6)
plt.plot(x, y7)
plt.plot(x, y8)
plt.plot(x, y9)
plt.plot(x, y10)
plt.plot(x, y11)
plt.plot(x, y12)
plt.plot(x, y13)
plt.plot(x, y14)
plt.plot(x, y15)
plt.plot(x, y16)
plt.plot(x, y17)
plt.bar(x, y)
plt.bar(x, y1)
plt.bar(x, y2)
plt.bar(x, y3)
plt.bar(x, y4)
plt.bar(x, y5)
plt.bar(x, y6)
plt.bar(x, y7)
plt.bar(x, y8)
plt.bar(x, y9)
plt.bar(x, y10)
plt.bar(x, y11)
plt.bar(x, y12)
plt.bar(x, y13)
plt.bar(x, y14)
plt.bar(x, y15)
plt.bar(x, y16)
#plt.bar(x, y17)

plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = x^n')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023015 LV 4 @ 2024-12-14 0:02:33

已修改

1.说明要绘制的函数，以及定义域x的范围:

我绘制的是心形螺旋函数;x的范围是-2<=x<=1/2.

2.截取绘制函数的图像。

4.提供绘制函数图像的代码:


import matplotlib.pyplot as plt
import numpy as np

def heart_spiral(theta):
    a = 1
    r = a * (1 - np.cos(theta))
    x = r * np.cos(theta)
    y = r * np.sin(theta)
    return x, y

theta_heart = np.linspace(0, 2 * np.pi, 500)

x_heart, y_heart = heart_spiral(theta_heart)

plt.plot(x_heart, y_heart, label='Heart Spiral')

plt.title("Two Interesting Spiral Functions")

plt.xlabel('x')

plt.ylabel('y')

plt.axis('equal')

plt.legend()

plt.show()

student2023037 LV 8 @ 2024-12-14 0:02:32

已修改

1.说明要绘制的函数，以及定义域x的范围。 f(x)=sin(x) f(x)=cos(x) -10<=x<=10

2.截取绘制函数的图像。 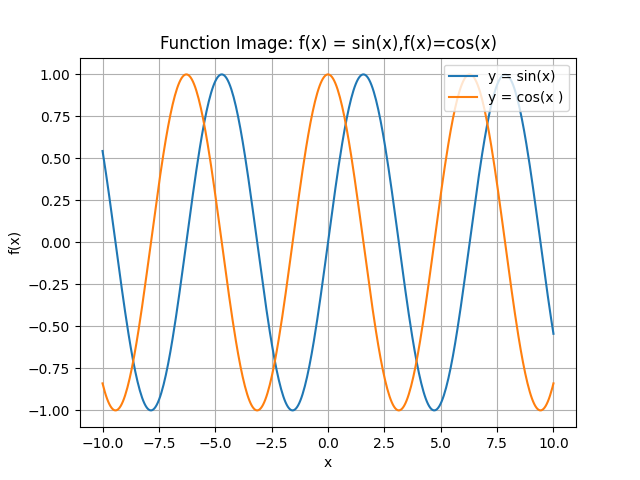3.说明你对函数图像的观察与思考。 sin (x) 与 cos (x) 都是周期函数，它们的值域都在 [-1,1] 之间，二者图像形状相似只是相位有差异。

4.提供绘制函数图像的代码。

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-10, 10, 400)  
y=np.sin(x)
y1 = np.cos(x )
plt.plot(x, y, label='y = sin(x)')
plt.plot(x, y1, label='y = cos(x )')
plt.legend(loc='upper right')
plt.xlabel('x')  
plt.ylabel('f(x)') 
plt.title('Function Image: f(x) = sin(x),f(x)=cos(x)')  
plt.grid()  
plt.show()

student2023007 LV 5 @ 2024-12-13 23:55:27

1说明要绘制的函数，以及定义域x的范围。代码中定义了四个正弦函数，它们分别是： y1 =sin(x)：这是基本的正弦函数 y2=sin(x+35)：这是一个正弦函数，其图像相对于 y1向左移动了35个单位 y=5sin(x)：这是一个振幅为5的正弦函数，振幅是基本正弦函数的5倍 y=2sin(x+120)：这是一个振幅为2的正弦函数，其图像相对于y1向左移动了120个单位定义域x的范围是从-5到50，共200个点，这意味着x的值将在这个区间内均匀分布。 2.截取绘制函数的图像:

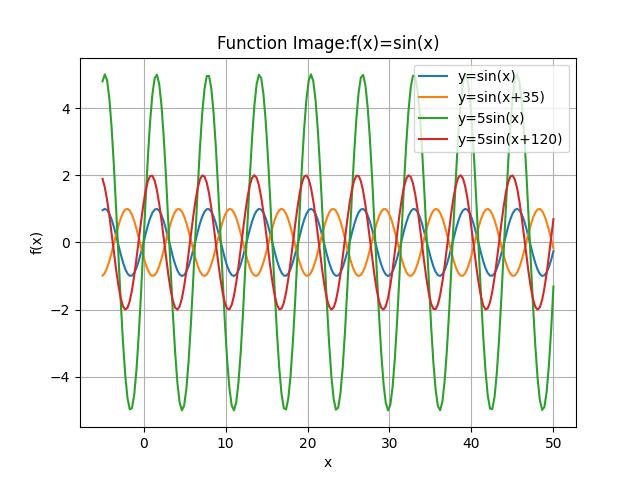
3.说明你对函数图像的观察与思考: 基本正弦波形： y1=sin⁡(x)的图像是一个标准的正弦波形，振幅为1，周期为2π。它在y轴上的范围是-1到1。相位移动： y2=sin⁡(x+35)和 y4=2sin⁡(x+120)的图像展示了正弦函数的相位移动。相位移动会影响波形的起始点，但不改变波形的形状和周期。振幅变化： y3=5sin(x)的图像展示了正弦函数振幅的变化。振幅的增加使得波峰和波谷的高度增加，但周期保持不变。y3的振幅是5，因此其波峰和波谷的高度是基本正弦波形的5倍。振幅和相位的组合： y4=2sin⁡(x+120)的图像展示了振幅和相位移动的组合效果。这个函数的振幅是2，并且向左移动了120个单位。周期性：所有这些函数都保持了正弦函数的基本周期性，即每2π单位重复一次。这种周期性是正弦函数的一个关键特性，它在许多自然现象和技术应用中都有体现。

student2023046 LV 3 @ 2024-12-13 23:29:21

已修改

1.绘制的函数

函数: y = sin(10/x)*x

取值: x为任意实数

2.函数的图像

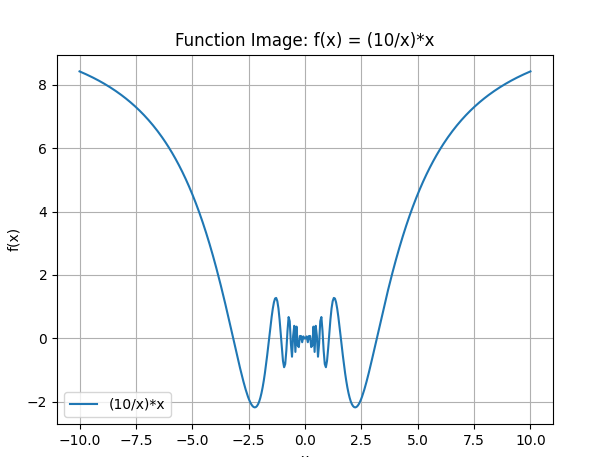
3.观察与思考

图像越往中间线条布局越密集，高度不断的减少，x轴也越来越小，线条平滑，无折角。

4.图像的代码

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-10,10,400)
y = np.sin(10/x)*x

plt.plot(x,y,label = '(10/x)*x')
plt.legend()

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Function Image: f(x) = (10/x)*x')
plt.grid()
plt.show()

student2023024 LV 5 @ 2024-12-13 23:28:30

函数：

y1=np.cos(x1) y2=np.sin(x1) y3=np.tan(x**9)

定义域：

-5<=x<=5

截取绘制函数的图像:

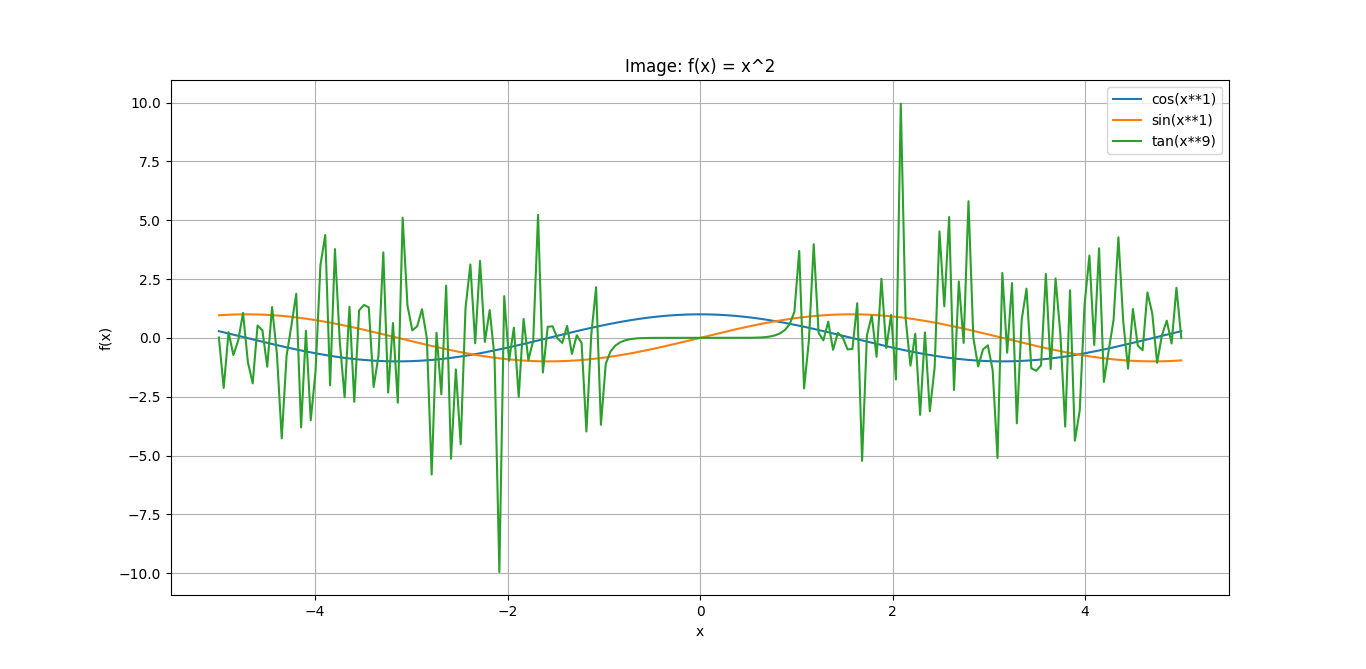cos(x1)和sin（x1）呈波浪形函数两个函数图像有周期性运动规律，tan（x**9）左右上下翻转，在-1至1的区间内图像与x轴重合，-1时迅速下降，1时又迅速上升，变化幅度较大。

代码

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(-5,5,200)
y1=np.cos(x**1)
y2=np.sin(x**1)
y3=np.tan(x**9)

plt.plot(x,y1,label="cos(x**1)")
plt.plot(x,y2,label="sin(x**1)")
plt.plot(x,y3,label="tan(x**9)")


plt.legend()
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Image: f(x) = x^2")
plt.grid()
plt.show()

student2023032 LV 4 @ 2024-12-13 23:27:11

已修改

1.绘制y=tan(x)函数图像，定义域：-2 * np.pi<x<2 * np.pi

2.绘制函数的图像:

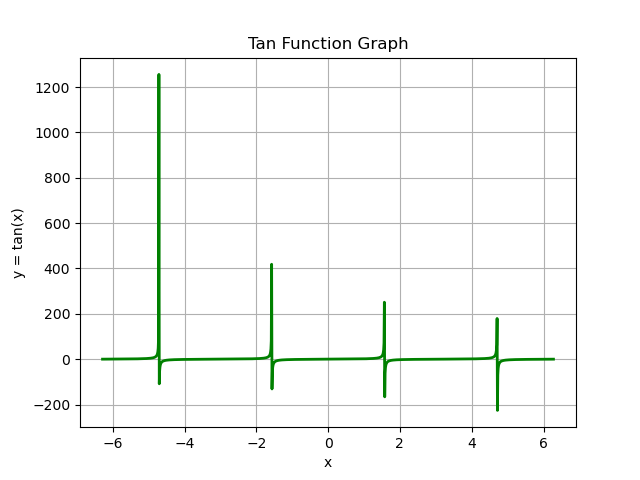
3.说明你对函数图像的观察与思考。

周期性

正切函数是周期函数，其最小正周期是π。这意味着每隔π个单位长度，函数的图像就会重复出现。

4.提供绘制函数图像的代码。

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-2 * np.pi, 2 * np.pi, 0.01)
with np.errstate(divide='ignore', invalid='ignore'):
    y = np.tan(x)
plt.plot(x, y, color='green', linewidth=2)
plt.title("Tan Function Graph")
plt.xlabel("x")
plt.ylabel("y = tan(x)")
plt.grid(True)
plt.show()

student2023043 LV 2 @ 2024-12-13 23:02:02

已修改

import numpy as np import matplotlib.pyplot as plt

def f(x): return np.sin(x)

x = np.linspace(-np.pi, np.pi, 100)
y = f(x)

plt.figure(figsize=(8, 6))

plt.plot(x, y)

plt.title('Sine Function')

plt.xlabel('x')

plt.ylabel('sin(x)')

plt.grid(True)

plt.axhline(0, color='black',linewidth=0.5)

plt.axvline(0, color='black',linewidth=0.5)

plt.show()

这段代码的核心原理是通过 numpy 生成数学函数的数据点，然后使用 matplotlib 将这些数据点绘制成图形。这种结合数学计算和图形绘制的方法是科学计算和数据分析中常用的技术，使得复杂的数学函数和数据集可以直观地展示和分析。

student2023001 LV 1 @ 2024-12-13 22:21:01

1.绘制三次函数这里示例为y = x^3，所以a = 1, b = 0, c = 0, d = 0

2.截取绘制函数的图像。

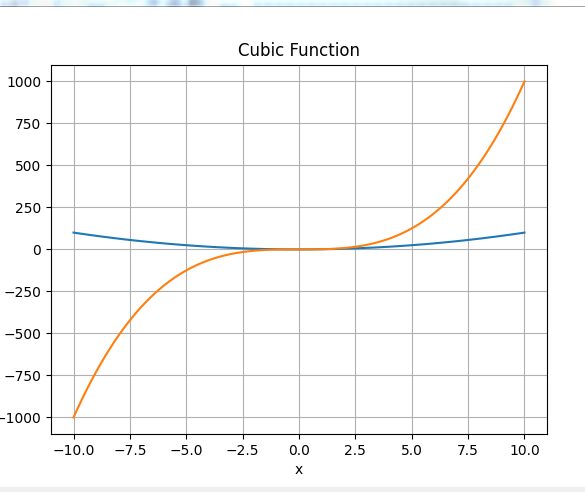
3.说明你对函数图像的观察与思考。

以下是对这段程序所绘制的函数图像（即三次函数y=x^3 的图像）的观察与思考：整体形状该函数图像呈现出一种独特的曲线形态，不同于一次函数的直线以及二次函数的抛物线形状。它具有明显的弯曲和延伸趋势，整体较为平滑，没有尖锐的拐角。

import numpy as np
import matplotlib.pyplot as plt
# 三次函数的系数，这里示例为y = x^3，所以a = 1, b = 0, c = 0, d = 0
a = 1
b = 0
c = 0
d = 0

# 生成x轴的数据，可以根据需求调整范围和点数
x = np.linspace(-10, 10, 100)
# 根据三次函数公式计算对应的y值
y = a * x ** 3 + b * x ** 2 + c * x + d

# 绘制图像
plt.plot(x, y)
# 设置图像标题
plt.title("Cubic Function")
# 设置x轴标签
plt.xlabel("x")
# 设置y轴标签
plt.ylabel("y")
# 显示网格，让图像更清晰直观
plt.grid(True)
# 显示图像
plt.show()

student2023031 LV 7 @ 2024-12-13 22:13:15

已修改

1. 说明要绘制的函数，以及定义域x的范围。

函数：y=cos(k) * sin(k * x)
定义域：x 可以取任意的实数

2.截取绘制函数的图像。

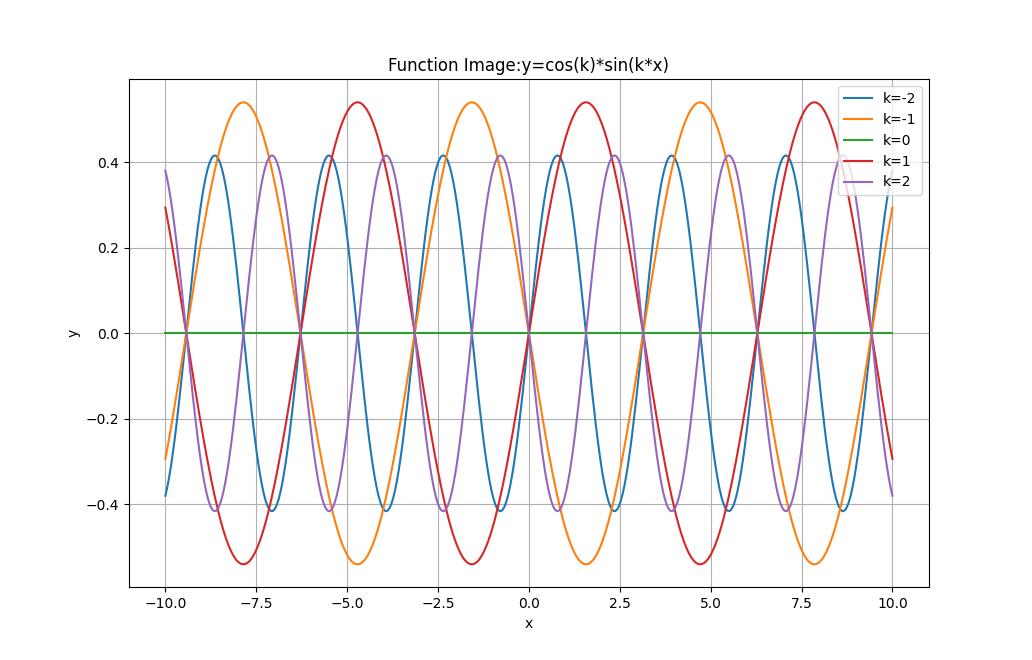
3.说明你对函数图像的观察与思考。

组成结构

此函数是由三角函数 cos(k) 与 sin(kx) 相乘构成的。其中 k 为常数。 cos(k) 的值是一个确定的常数，它起到对 sin(kx) 进行伸缩的作用。而 sin(kx) 是一个周期函数，其周期会随着 k 值的变化而改变。

对称轴

函数图像关于 X轴对称，这意味着在对称轴两侧等距离的点对应的函数值是相等的。

特殊点

当 x = 0 时， y=cos(k) * sin(0) = 0，所以函数图像必然经过原点 (0,0)。

4.提供绘制函数图像的代码。

import numpy as n
import matplotlib.pyplot  as plt
x = n.linspace(-10, 10, 400)  # 从-10到10之间生成400个点

for k in range(-2,3,1):
    y = n.cos(k)*n.sin(k*x)
    plt.plot(x, y, label='k='+str(k))

plt.legend()
plt.xlabel('x')  # x轴标签
plt.ylabel('y')  # y轴标签
plt.title('Function Image:y=cos(k)*sin(k*x)')  # 图像标题
plt.grid()
plt.show()

student2023017 LV 3 @ 2024-12-13 22:11:13

已修改

一、函数、定义域说明

在自由落体运动中，下落高度 $h$ 与时间 $t$ 的关系可以用函数 $h(t)=\frac{1}{2}gt^2$ 来表示,这里 $g$ 是重力加速度，通常取 $g=9.8m/s^2$ 。

定义域 $t$ 的范围，因为时间不能为负，所以这里我们取 $t\in[0,10]$ （单位：秒），这个范围表示从开始下落计时，到经过 10 秒的这段时间内物体下落高度随时间的变化情况。

二、函数图像截图

三、对函数图像的观察与思考

单调性：

从图像可以看出，函数在定义域 $[0,10]$ 上是单调递增的，这符合实际物理意义，随着时间的推移，物体下落的高度必然是不断增加的，时间越长，下落的距离越远。
形状特点：

它是一个抛物线形状，这是因为函数是二次函数的形式，二次项系数大于 0，抛物线开口向上。而且下落高度与时间的平方成正比，时间对高度的影响随着时间增大变得更加显著，反映在图像上就是曲线上升的趋势越来越陡。

四、绘制函数图像的代码

import matplotlib.pyplot as plt
import numpy as np

g = 9.8 
t = np.linspace(0, 10, 500)  
# 根据函数关系计算对应的高度值
h = 0.5 * g * t ** 2  

plt.plot(t, h)
plt.xlabel('Time (s)')
plt.ylabel('Height (m)')
plt.title('Height vs Time in Free Fall')
plt.show()

👍 1

student2023023 LV 5 @ 2024-12-13 22:10:53

1、x 的范围是从 -10 到 10，一共生成 400 个等间隔的值。

2、函数图像：

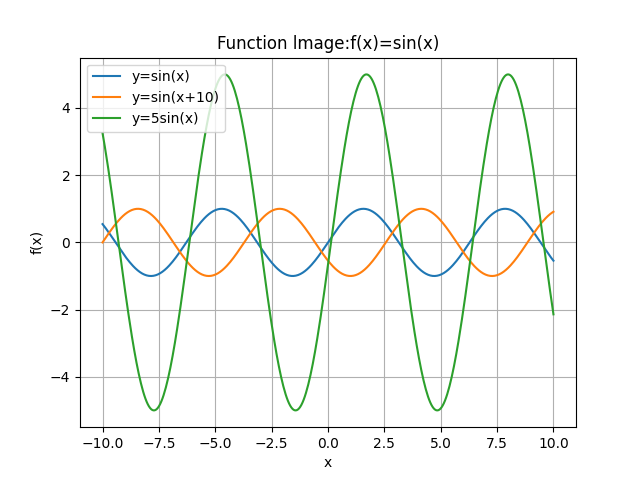
3、观察：首先，用代码画函数图像很神奇，只要改一下函数定义就能画出不同的图像。而且还能调整图像的范围和精细程度。图像上有坐标轴标签、标题和网格线，看起来很清楚。这个方法能画很多种数学函数的图像呢。

思考：在学习中，画函数图像能帮我更好地理解函数的性质。我可以自己试着写代码画函数图像，这样能加深对函数和编程的认识。以后做数据分析说不定也能用得上函数图像，比如看看数据的趋势。我还在想怎么能让图像更好看，也希望能学到更多关于用代码画图像的技巧。

4、代码：

import matplotlib.pyplot as plt import numpy as np #数据点 x=np.linspace(-10,10,400) y1=np.sin(x) y2=np.sin(x+10) y3=5*np.sin(x+25) #绘制图像 plt.plot(x,y1,label='y=sin(x)') plt.plot(x,y2,label='y=sin(x+10)') plt.plot(x,y3,label='y=5sin(x)') plt.legend() plt.xlabel('x') plt.ylabel('f(x)') plt.title('Function lmage:f(x)=sin(x)') plt.grid() plt.show()

student2023052 LV 4 @ 2024-12-13 21:52:07

已修改

1.要绘制的函数以及定义域x的范围：

三个三角函数（正弦cin、余弦cos、正切tan） x[0,2π]

2.截取绘制函数的图像：

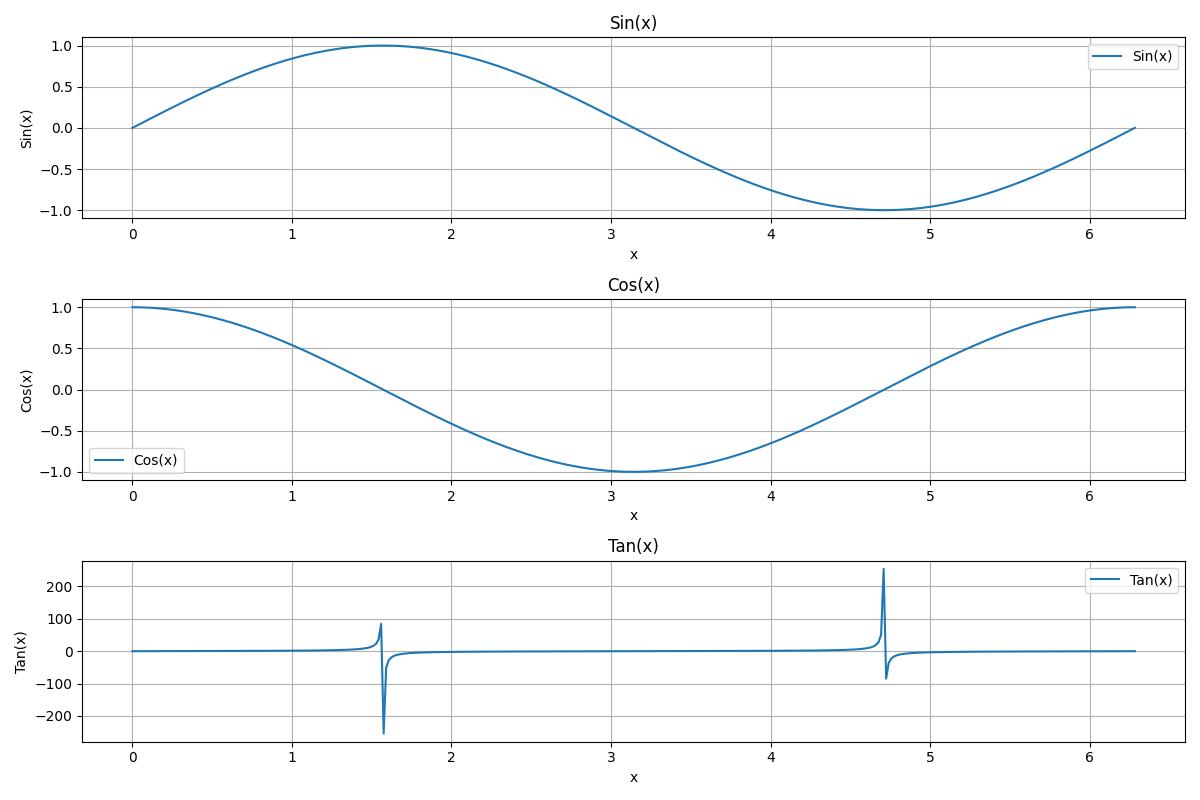
3.你对函数图像的观察与思考：

正弦函数 ( \sin(x) )：

波形：正弦函数的图像是一个波形，它在 ( x = 0 ) 时从0开始，上升到 ( x = \frac{π}{2} ) 时达到最高点1，然后下降到 ( x = π ) 时达到最低点-1，再上升到 ( x = \frac{3π}{2} ) 时回到0，最后在 ( x = 2π ) 时完成一个周期。

周期性：正弦函数是周期性的，每 ( 2π ) 重复一次，这意味着每过 ( 2π ) 单位，函数值会重复。

对称性：正弦函数关于原点对称，即 ( \sin(-x) = -\sin(x) )。

余弦函数 ( \cos(x) )：

波形：余弦函数的图像也是一个波形，但它在 ( x = 0 ) 时从1开始，下降到 ( x = π ) 时达到最低点-1，然后上升到 ( x = 2π ) 时回到1，完成一个周期。

周期性：和正弦函数一样，余弦函数也是周期性的，每 ( 2π ) 重复一次。

对称性：余弦函数关于y轴对称，即 ( \cos(-x) = \cos(x) )。

正切函数 ( \tan(x) )：

波形：正切函数的图像在 ( x = \frac{π}{2} ) 和 ( x = \frac{3π}{2} ) 处有垂直渐近线，这意味着在这些点函数值会趋向于正无穷或负无穷。在这两个渐近线之间，正切函数的值从负无穷增加到正无穷。

周期性：正切函数是周期性的，周期为 ( π )，但因为存在渐近线，所以它的图像在每个周期内是不连续的。

对称性：正切函数没有简单的对称性，但它是奇函数，即 ( \tan(-x) = -\tan(x) )。

4.绘制函数图像的代码：

import numpy as np
import matplotlib.pyplot as plt

# 定义x的范围
x = np.linspace(0, 2 * np.pi, 400)

# 计算三角函数的值
sin_x = np.sin(x)
cos_x = np.cos(x)
tan_x = np.tan(x)

# 绘制图像
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(x, sin_x, label='Sin(x)')
plt.title('Sin(x)')
plt.xlabel('x')
plt.ylabel('Sin(x)')
plt.grid(True)
plt.legend()

plt.subplot(3, 1, 2)
plt.plot(x, cos_x, label='Cos(x)')
plt.title('Cos(x)')
plt.xlabel('x')
plt.ylabel('Cos(x)')
plt.grid(True)
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(x, tan_x, label='Tan(x)')
plt.title('Tan(x)')
plt.xlabel('x')
plt.ylabel('Tan(x)')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

student2023036 LV 8 @ 2024-12-13 21:10:04

已修改

1.说明要绘制的函数，以及定义域x的范围。

y=cos(x)函数及其变换,-5<x<5

2.截取绘制函数的图像。

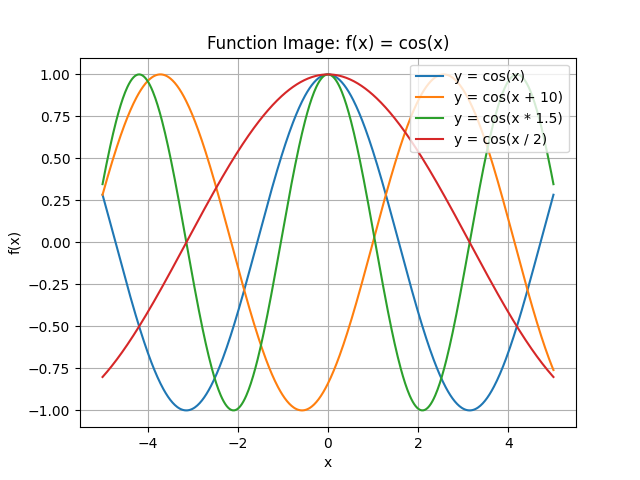
3.说明你对函数图像的观察与思考。

(1) y=cos(x): 基本余弦函数，有周期性，周期为2π，关于y轴对称 (2) y=cos(x+10): 基本余弦函数向左平移得到的，平移不改变函数的形状和周期，只是在水平方向上移动了位置。 (3) y=cos(x*1.5) 与 y=cos(x/2): 基本余弦函数系数改变。周期发生变化，对于 cos(a·x)类函数，周期为2π/a

4.提供绘制函数图像的代码。

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-5, 5, 600)  # 从-10到10之间生成400个点
y = np.cos(x)
y1 = np.cos(x + 10)
y2 = np.cos(x * 1.5)
y3 = np.cos(x / 2)
y5 = np.cos(x)

# 绘制图像
plt.plot(x, y, label='y = cos(x)')
plt.plot(x, y1, label='y = cos(x + 10)')
plt.plot(x, y2, label='y = cos(x * 1.5)')
plt.plot(x, y3, label='y = cos(x / 2)')

# 通过loc参数设置图例位置为右上角
plt.legend(loc='upper right')

plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = cos(x)')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023050 LV 3 @ 2024-12-13 20:58:54

图像截图：

轴的范围大约是从到每个函数的图像在这个定义域内呈现出螺旋状的曲线图中用不同颜色表示了三个函数：蓝色（Function 1）橙色（Function 2）绿色（Function 3）这些函数的图像在轴的范围从到之间绘制，展示了函数在这个定义域内的特性。

代码：

student2023030 LV 6 @ 2024-12-13 20:36:44

已修改

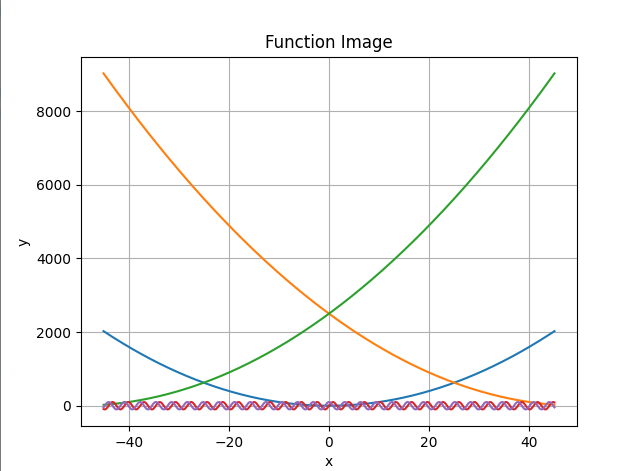1.函数解释及定义域 函数一：二次函数函数二：二次函数函数三：二次函数函数四：是一个正弦函数，其振幅为100，周期T等于Π 函数五：属于余弦函数

2.代码

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(-45,45,700)
y1=x**2
y2=(x-50)**2
y3=(x+50)**2
y4=100*np.sin(x*2)
y5=100*np.cos(x*2)

plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
plt.plot(x,y4)
plt.plot(x,y5)

plt.xlabel("x")
plt.ylabel("y")
plt.title("Function Image")
plt.grid()

plt.show()

student2023012 LV 7 @ 2024-12-13 18:49:19

已修改

1.说明要绘制的函数，以及定义域x的范围。

y4 = (100-x**2)0.5 与 y5 = -(100-x2)**0.5

-10<=x<10

2.截取绘制函数的图像。

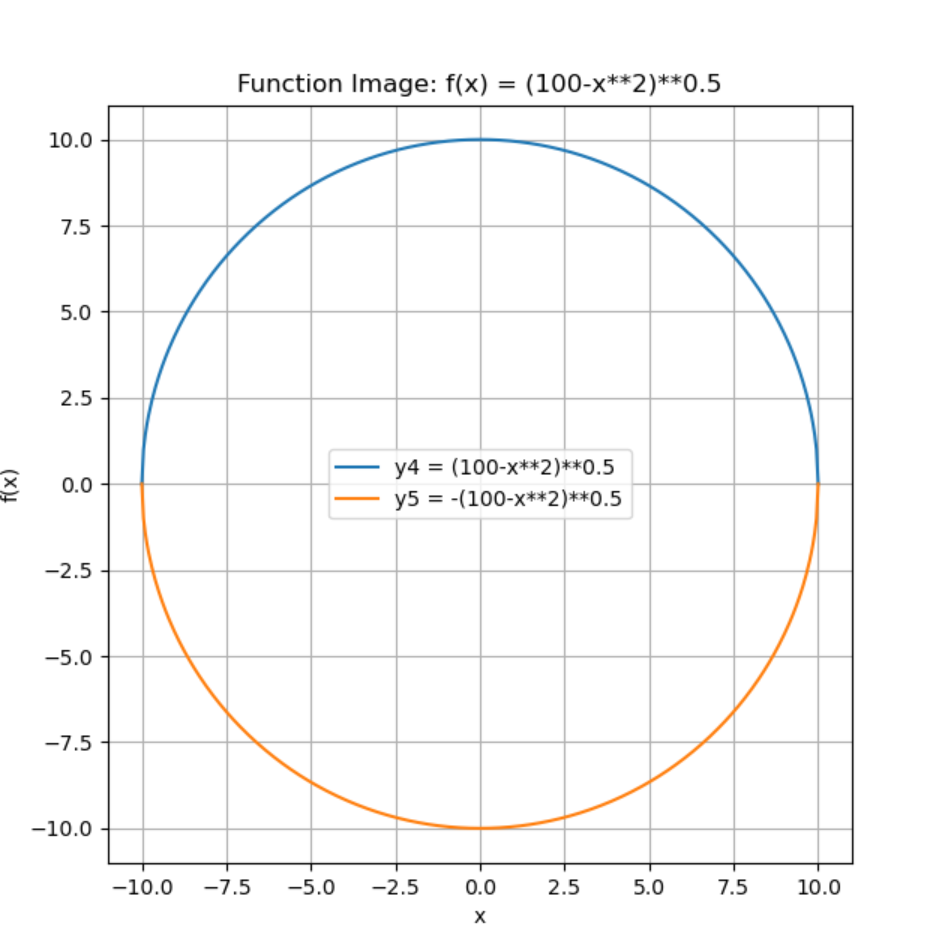
3.说明你对函数图像的观察与思考。

这是一个圆的函数。根据圆的定义：在一平面内到一点距离相等的所有点的集合，我通过坐标系中的距离公式，确定一些到原点距离为10的点的位置，并将它们连起来，就会得到一个圆。

4.提供绘制函数图像的代码。

import numpy as np

# 创建数据点
x = np.linspace(-10, 10, 400)  # 从-10到10之间生成400个点
y4 = (100-x**2)**0.5
y5 = -(100-x**2)**0.5


# 绘制图像
plt.plot(x,y4,label='y4 = (100-x**2)**0.5')
plt.plot(x,y5,label='y5 = -(100-x**2)**0.5')
plt.legend() #添加图例


plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = (100-x**2)**0.5')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023010 LV 5 @ 2024-12-13 18:47:29

已修改

1.绘制一次函数 y = 3x - 2，定义域 x 范围为 [-5, 5] 2.

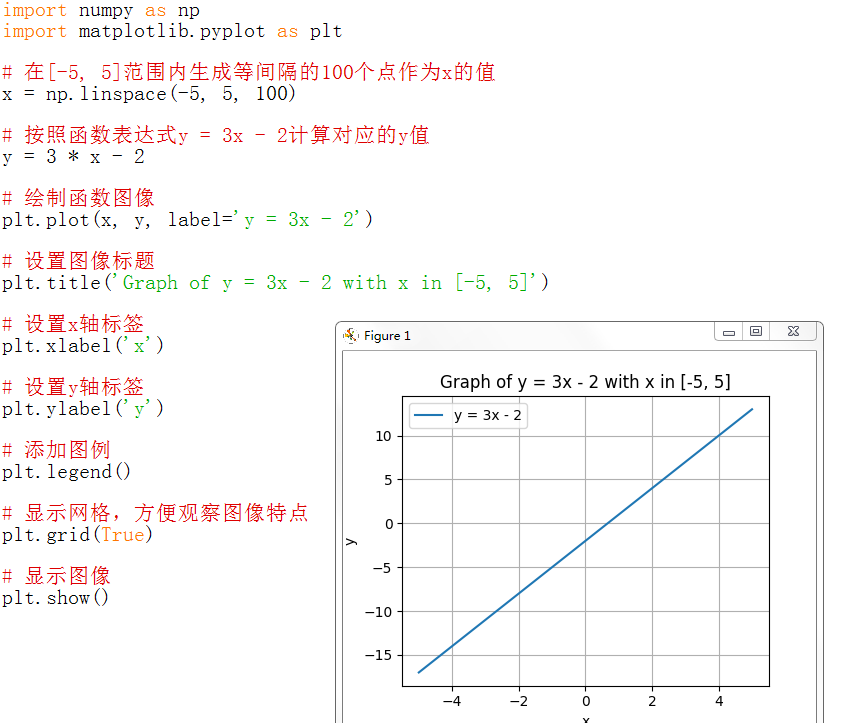
截距情况：函数中的常数项-2是直线在y轴上的截距，也就是当x = 0时，y的值。从图像上看，直线与y轴相交于点(0, -2)，截距反映了函数图像相对于坐标原点的位置关系，负的截距表明直线与y轴的交点在y轴的负半轴上。代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5, 5, 100)
y = 3 * x - 2
plt.plot(x, y, label='y = 3x - 2')
plt.title('Graph of y = 3x - 2 with x in [-5, 5]')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

student2023040 LV 4 @ 2024-12-13 18:46:06

已修改

1.说明要绘制的函数，以及定义域x的范围： 正弦函数图像，在-1~1之间取400个点。

2.截取绘制函数的图像：

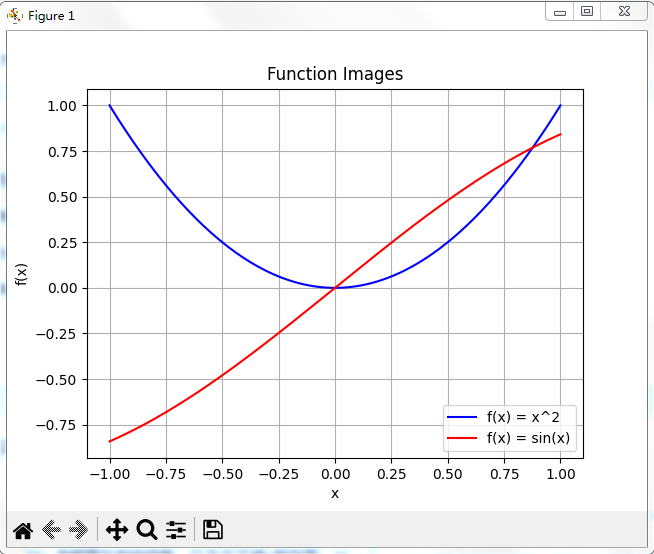
3.说明你对函数图像的观察与思考：

从代码中可知，自变量 x 的取值范围通过 np.linspace(-1, 1, 400) 被设定在 [-1, 1] 区间内。对于 y1 = x ** 2，其值域在 [0, 1] 这个区间内，因为 x 在 [-1, 1] 取值时，平方后最小为 0（当 x = 0 时），最大为 1（当 x = ±1 时）。而对于 y2 = np.sin(x)，其值域在 [-sin(1), sin(1)] 区间内，由于 sin 函数的值域本身是 [-1, 1]，这里 x 限定在 [-1, 1] ，所以对应的值域是上述区间。

4.提供绘制函数图像的代码：

import numpy as np

x = np.linspace(-1, 1, 400)

y1 = x ** 2

y2 = np.sin(x)

plt.plot(x, y1, label='f(x) = x^2', color='blue')

plt.plot(x, y2, label='f(x) = sin(x)', color='red')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Function Images')
plt.grid()

plt.legend()
plt.show()

student2023005 LV 3 @ 2024-12-13 18:44:56

绘制的图像：y=1/(x^2-1) （囧函数） 1.定义域-5<=x<=5 2.绘制的函数图像如下图： 3.我的观察与思考：囧函数” 通常是指形如y=1/(x^2-1)的函数（类似具有特定形状类似 “囧” 字的函数表达式）因为对于任意实数x,x^2+1，恒大于0，分母不为0，函数均有定义。函数是偶函数，关于y轴对称 4.```python

import numpy as np
import matplotlib.pyplot as plt
a=2
x = np.linspace(-5, 5, 1000)

y=1/(x**2-1)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('y=1/(x**2-1)')
plt.grid()
plt.show()

student2023041 LV 6 @ 2024-12-13 18:44:46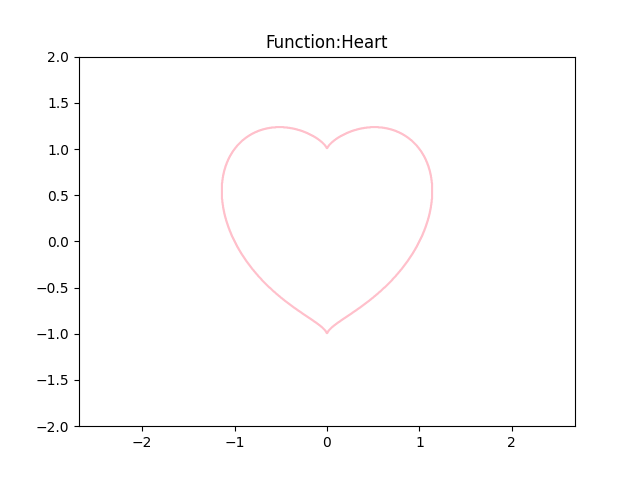

import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(-2,2,1000)
y=np.linspace(-2,2,1000)

X,Y=np.meshgrid(x,y)

F=(X**2+Y**2-1)**3-X**2*Y**3

mask=F<=0

plt.contour(X,Y,mask,colors='pink',linewidths=1.5)

plt.title("Function:Heart")
plt.axis('equal')
plt.show()

student2023009 LV 4 @ 2024-12-13 18:44:45

已修改

绘制f(x) = sin(nx)的图像，范围是-2π到2π之间

2.

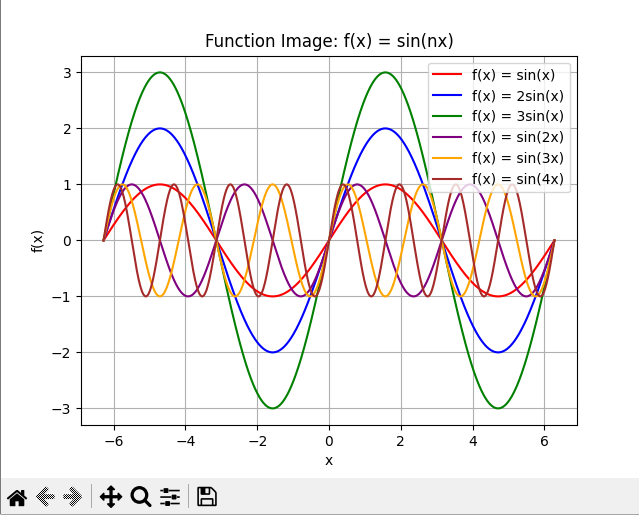
3.说明你对函数图像的观察与思考：图像关于原点对称，体现了正弦函数的奇偶性特点

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-2 * np.pi, 2 * np.pi, 1000)  # 从-2π到2π之间生成1000个点

# 定义不同的正弦函数
y1 = np.sin(x)                # f(x) = sin(x)
y2 = 2 * np.sin(x)            # f(x) = 2sin(x)
y3 = 3 * np.sin(x)            # f(x) = 3sin(x)
y4 = np.sin(2 * x)            # f(x) = sin(2x)
y5 = np.sin(3 * x)            # f(x) = sin(3x)
y6 = np.sin(4 * x)            # f(x) = sin(4x)

# 绘制图像
plt.plot(x, y1, label='f(x) = sin(x)', color='red')       
plt.plot(x, y2, label='f(x) = 2sin(x)', color='blue')      
plt.plot(x, y3, label='f(x) = 3sin(x)', color='green')     
plt.plot(x, y4, label='f(x) = sin(2x)', color='purple')     
plt.plot(x, y5, label='f(x) = sin(3x)', color='orange')     
plt.plot(x, y6, label='f(x) = sin(4x)', color='brown')    

# 设置标签和标题
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = sin(nx)')  # 图像标题

# 添加网格
plt.grid(True)

# 添加图例
plt.legend()

# 显示图像
plt.show()

student2023038 LV 2 @ 2024-12-13 18:44:42

绘制f(x)=2x^3的图像，观察其中变化规律。

定义域-10<=x<=10(n为整数)

绘制的函数图像如下图：

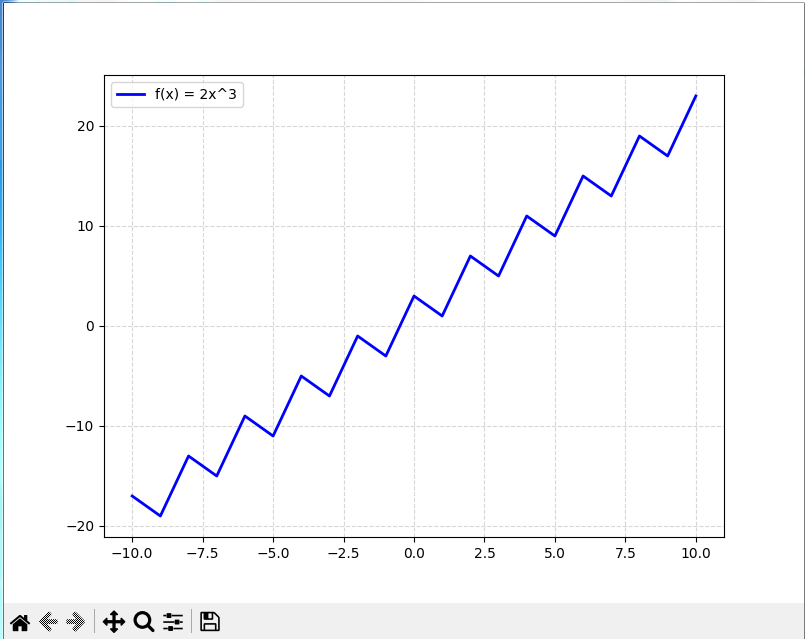
我的观察与思考：

单调性：当x<0,f'(x)=6x^2>0,函数单调递减。当x>0,f'(x)=6x^2>0,函数单调递增。凹凸性：当x<0,f''(x)=12x>0,函数图像凹向下。当x<0,f''(x)=12x>0,函数图像凹向上。当x=0 处，函数图像有一个拐点。渐近性：该函数没有水平、垂直或斜渐近线，因为当x趋向于无穷大或负无穷大时， f(x) 也趋向于无穷大或负无穷大。绘制的函数的代码：

import matplotlib.pyplot as plt

# 定义函数
def f(x):
    return 2 * x ^ 3

# 生成 x 的取值范围
x_values = range(-10, 11)  # 从 -10 到 10 的整数

# 计算对应的 y 值
y_values = [f(x) for x in x_values]

# 创建图形和坐标轴
plt.figure(figsize=(8, 6))  # 设置图形大小

# 绘制函数图像
plt.plot(x_values, y_values, label='f(x) = 2x^3', color='blue', linewidth=2)

# 添加网格
plt.grid(True, linestyle='--', alpha=0.5)

# 添加图例
plt.legend()

# 显示图像
plt.show()

student2023022 LV 6 @ 2024-12-13 18:43:30

已修改

绘制y=cosx^n的图像，观察其中变化规律。

1.定义域-1<=x<=1.25,n的值1~10变化。

2.绘制的函数图像如下图：

3.我的观察与思考：单调性：n从1到10都是差不多的形状，只是值的略微变化密集性：在x>1时，线条会变得密集而不重合对称性：以x=0为轴，线条向两方向对称 4.绘制的函数的代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1.25, 1.25, 600)
y1 =np.cos(x)
y2 =np.cos(x**2)
y3 =np.cos(x**3)
y4 =np.cos(x**4)
y5 =np.cos(x**5)
y6 =np.cos(x**6)
y7 =np.cos(x**7)
y8 =np.cos(x**8)
y9 =np.cos(x**9)
y10 =np.cos(x**10)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y4)
plt.plot(x, y5)
plt.plot(x, y6)
plt.plot(x, y7)
plt.plot(x, y8)
plt.plot(x, y9)
plt.plot(x, y10)
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Image')  # 图像标题
plt.grid()
plt.show()

student2023019 LV 8 @ 2024-12-13 18:43:06

已修改

绘制y=nx+(n-1)/x（对勾函数）的图像，观察其中的规律

1.定义域-20<=x<=20,1<=n<=4(n为正整数)

2.绘制的图像如下

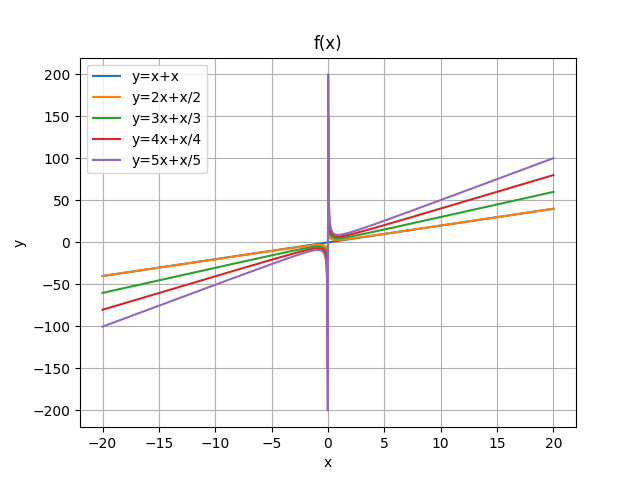
3.我的思考

（1）.当x=0时函数无定义

（2）.当x趋近于0函数值趋近于正无穷或负无穷

（3）.函数关于原点对称

（4）.整体形状为对勾状

4.绘制的图像代码：

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(-20,20,1000)
y=x+x
y2=2*x+1/x
y3=3*x+2/x
y4=4*x+3/x
y5=5*x+4/x
plt.plot(x,y,label='y=x+x')
plt.plot(x,y2,label='y=2x+1/x')
plt.plot(x,y3,label='y=3x+2/x')
plt.plot(x,y4,label='y=4x+3/x')
plt.plot(x,y5,label='y=5x+4/x')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x)')
plt.grid()
plt.show()

student2023018 LV 7 @ 2024-12-13 18:42:22

绘制f(x)=x²+1/x²的图像,观察其中变化规律。 1.定义域为-10≤x≤10（x≠0）. 2.绘制的函数图像如下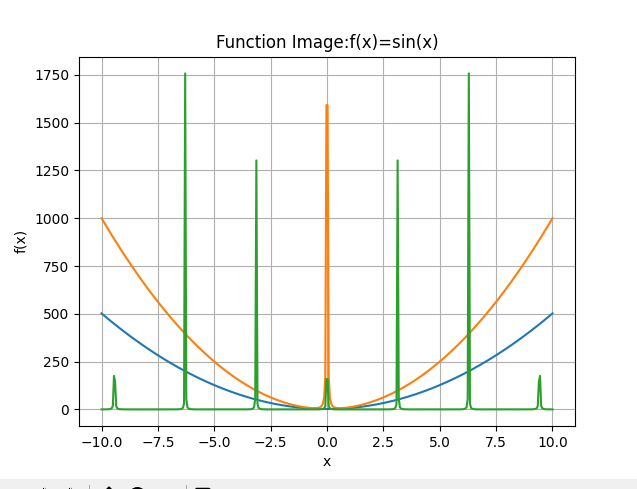： 3.我的观察与思考：对称性：图像关于y轴对称，是偶函数。增长性：函数总是成爆炸式增长。 4.绘制的函数的代码：

import matplotlib.pyplot as p
import numpy as np
x=np.linspace(-10,10,400)
y1=x*x*5+2
y2=10*x*x+1/(x*x)
y3=(np.cos(x*3)/np.tan(x*2))/(np.sin(x)*5)

p.plot(x,y1,label='y=x*x')
p.plot(x,y2,label='y=x*x+1/x*x')
p.plot(x,y3,label='y=cos(x)/tan(x)/sin(x)')
#p.legend()

p.xlabel('x')
p.ylabel('f(x)')
p.title('Function Image:f(x)=sin(x)')
p.grid()
p.show()

student2023051 LV 6 @ 2024-12-13 18:41:55

已修改

绘制y=sin(10*x)/x的图像 代码：

import numpy as n
x=n.linspace(-10,10,500)
y=n.sin(10*x)/x
p.plot(x,y)
p.xlabel('x')
p.ylabel('f(x)')
p.title('...')
p.grid()
p.show()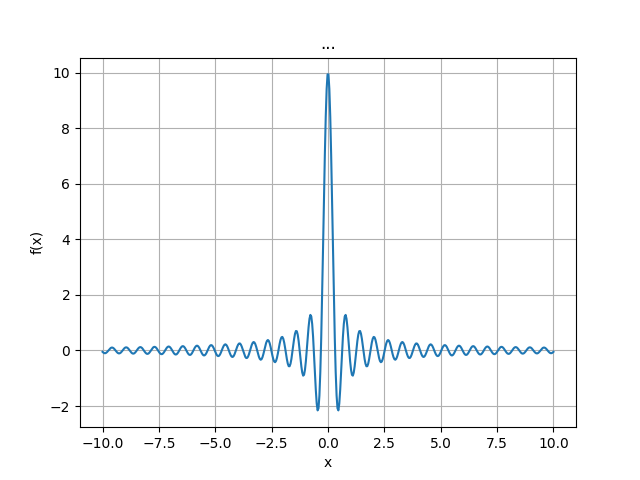

分析：

通过求解的驻点以及结合单调性变化，可以确定函数的极值点情况，在极值点处函数取得极值。由于函数定义域为且没有明显边界限制，所以函数不一定存在最大值和最小值，需要综合考虑在整个定义域内函数的变化情况来判断最值是否存在。综上所述，函数具备上述诸多性质特点，进一步深入分析其驻点等情况能更细致地把握它在不同区间上的具体表现。

student2023016 LV 1 @ 2024-12-13 18:41:39

1.绘制的函数：

1.正弦函数 2.余弦函数 3.x**2

2.图片：

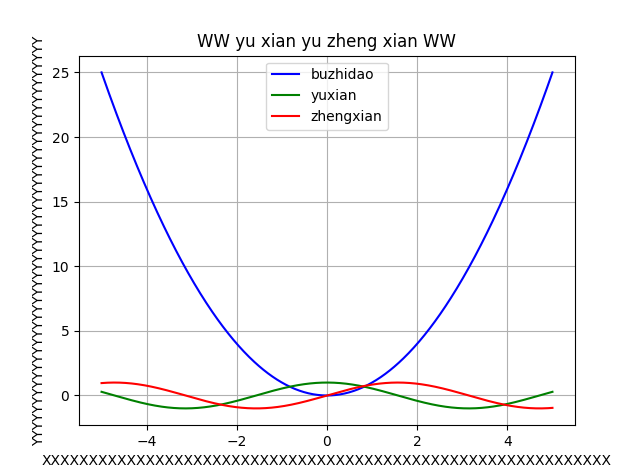
3.思考：

4.代码：

import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 600)
y_c = np.cos(x)
y_s = np.sin(x)
y_a = x**2
plt.plot(x, y_a, label='buzhidao', color='blue')
plt.plot(x, y_c, label='yuxian', color='green')
plt.plot(x, y_s, label='zhengxian', color='red')
plt.xlabel('XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX')
plt.ylabel('YYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY')
plt.title('WW yu xian yu zheng xian WW')
plt.legend()
plt.grid()
plt.show()

student2023027 LV 4 @ 2024-12-13 18:40:46

绘制y=x^n的图像，观察其中变化规律。

1.定义域-3<=x<=3,n的值0到3到9到18到30到45变化。

2.绘制的函数图像如下图：

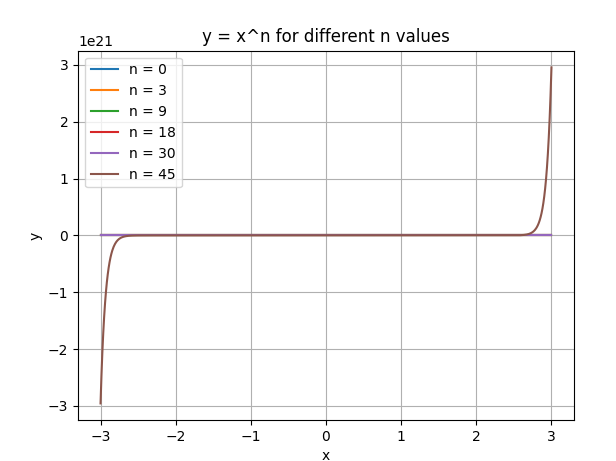
3.我的观察与思考：

随着n值不断变大，在|x| < 1的区间内，函数值越来越趋近于0（除了n = 0情况），曲线更加贴近x轴；而在|x| > 1的区间内，函数值随x绝对值的增大而迅速增大，曲线变得越来越陡峭，并且奇偶性决定了曲线关于原点对称（奇数n时）还是关于y轴对称（偶数n时）的特征。

3.绘制的函数的代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 1000)
n_values = [0, 3, 9, 18, 30, 45]
for n in n_values:
    y = x ** n
    plt.plot(x, y, label=f'n = {n}')

plt.xlabel('x')
plt.ylabel('y')
plt.title('y = x^n for different n values')
plt.legend()
plt.grid(True)
plt.show()

student2023044 LV 4 @ 2024-12-13 18:40:24

1.说明要绘制的函数，以及定义域x的范围:

连贯的半椭圆形；定义域x的范围：-10<x<10

2.截取绘制函数的图像:

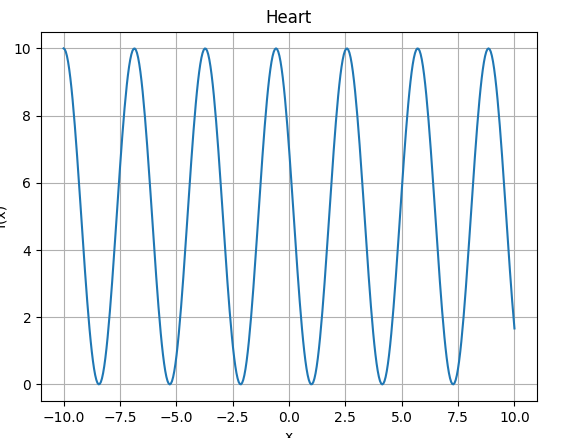
3.说明你对函数图像的观察与思考:

1.当y的cos的值为次方再乘以一个任意值时，所呈现出来的是一个有规律的图形。 2.所呈现出的图形都是等高等低，几个全等的不规则图形

4.提供绘制函数图像的代码：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10,10,400)
y =10 * np.cos(x+10) ** 2
plt.title("Heart")
plt.plot(x, y)
plt.grid()
plt.xlabel('x')  
plt.ylabel('f(x)') 
plt.show()

student2023034 LV 3 @ 2024-12-13 18:40:09

已修改

student2023045 LV 2 @ 2024-12-13 18:39:48

已修改

一 1.函数：阿基米德螺线

2.定义域x的范围：

theta的范围是从0到2*pi

x = r * np.cos(theta)

r = a * np.cos(n * theta)

注：cos是余弦

二.绘制函数的图像：

三.对函数图像的观察与思考：

1.数学意义

为数学分析、几何研究等提供了多样的对象和方法.

2.实际应用

(1)工程领域：

在凸轮设计、车床卡盘设计、涡旋弹簧、螺纹、蜗杆设计中应用较多。例如，基于阿基米德螺旋曲线设计制作风道，可以让排风按照最佳路线运行，提高效率与稳定性，如能率高抗风热水器的风道设计就是利用了这一原理.

(2)农业领域：

阿基米德发明的圆筒状螺旋扬水器，也就是 “阿基米德螺旋”，被广泛应用于灌溉，至今仍在埃及等地使用，解决了用尼罗河水灌溉土地的难题.

四.代码：

import numpy as np
import matplotlib.pyplot as plt
a = 0  
b = 1  
theta = np.linspace(0, 10 * np.pi, 1000)
r = a + b * theta
x = r * np.cos(theta)
y = r * np.sin(theta)
fig, ax = plt.subplots(figsize=(6, 6))
ax.plot(x, y)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_title("Archimedes' Spiral")
plt.show()

student2023013 LV 4 @ 2024-12-13 18:38:04

1和2.说明要绘制的函数，以及定义域x的范围。

以及

截取绘制函数的图像。

当x = np.linspace(-2, 2, 400) ![] 当x = np.linspace(-1, 1, 400)

3.说明你对函数图像的观察与思考。

#绘制x的平方函数图像 plt.plot(x, power_2)
#绘制x的四次方函数图像 plt.plot(x, power_4)
#绘制x的六次方函数图像 plt.plot(x, power_6)
#绘制sin(x^8 + 10)函数图像 plt.plot(x, sin_compound)
#绘制cos(x^8)函数图像 plt.plot(x, cos_compound)
#绘制tan(x^3)函数图像 plt.plot(x, tan_compound)

4.提供绘制函数图像的代码。

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-2, 2, 400)  # 从-10到10之间生成400个点
y = x**2
y1 = x**4
y2 = x**6
y3 = np.sin(x**8+10)
y5 = np.cos(x**8)
y10 = np.tan(x**3)

# 绘制图像
plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y5)
plt.plot(x, y10)
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = x^n')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023006 LV 6 @ 2024-12-13 18:37:39

已修改

绘制f(x)=cos(x2)和f(x)=sin(x2)的图像 1.定义域-10<=x<=10

2.绘制的函数图像如下图：

3.我的观察与思考： 对称性： 两个函数都表现出了关于 y 轴的对称性。 振幅变化： 两个函数的振幅在 x 轴的正负方向上保持不变，因为正弦和余弦函数的振幅是固定的。

函数的增长和衰减： 由于 x**2 的增长，函数的增长和衰减速度在 x 远离 0 时加快。这导致函数在 x 轴两端的波动变得更加稀疏。

3.绘制的函数的代码：


import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(-10,10,10)
y1=np.sin(x**2)
y2=np.cos(x**2)
plt.plot(x,y1,label="sin(x**2)")
plt.plot(x,y2,label="cos(x**2)")
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)') 
plt.title('Function Image: f(x) = x^n')
plt.grid()
plt.show()

student2023021 LV 7 @ 2024-12-13 18:37:02

已修改

1.函数一：y=sin(x)

函数二：y=9sin(x+30)

函数三：y=3sin(x)

定义域的范围：定义域x的范围是从-30到20，生成了300个等间距的点来作为函数图像绘制时x的取值。

2. 截取绘制函数的图像如下图：

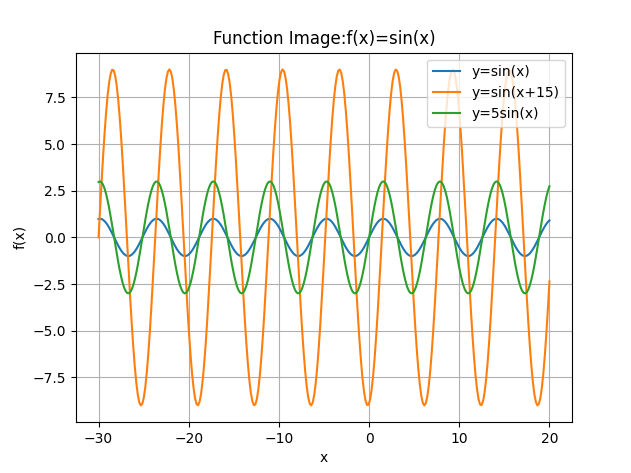
3.我的观察与思考： 函数y=sin(x)像有规律的波浪，高低在到间，在到里有好多重复波浪，还关于原点对称。函数前面乘数字会改变波浪高低，加数字会让波浪左右移

3.绘制的函数的代码：

import matplotlib.pyplot as plt
import numpy as np
x=np.linspace(-30,20,300)
y1=np.sin(x)
y2=9*np.sin(x+30)
y3=3*np.sin(x)
plt.plot(x,y1,label='y=sin(x)')
plt.plot(x,y2,label='y=sin(x+15)')
plt.plot(x,y3,label='y=5sin(x)')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Function Image:f(x)=sin(x)')
plt.grid()
plt.show()

student2023004 LV 6 @ 2024-12-13 18:35:45

已修改

绘制f(x) = cos(x)//f(x) = cos(x) * sin(x)的图像 1.定义域 -10 <= x <= 10 2.观察：观察sin(x)*cos(x)的波动情况 cos(x)会在范围 -1<=x<=1 中随y的增大而产生波动相应cos(x-5)会在相同范围中随y的增大而产生波动,但波峰和波谷所对应y的值增加了0.5; cos(x) × sin(x) 会呈cos(x)约0.5y倍长的波，但波的范围增大至-3 <= x <= 3；而cos(x-5) × sin(x)呈相同图像图像：

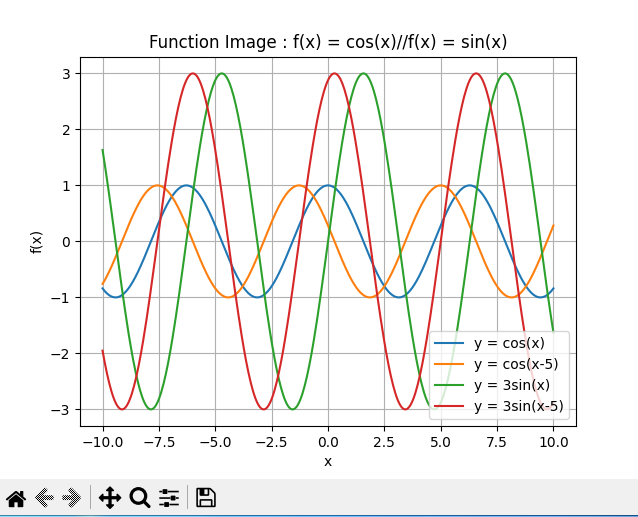
当y = cos(x)*sin(x)时

绘制代码：

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace( -10,10,400)
y1 = np.cos(x)
y2 = np.cos(x-5)
y3 = np.sin (x)
y4 =np.cos(x) * np.sin (x)
plt.plot(x,y1,label = "y = cos(x)")
plt.plot(x,y2,label = "y = cos(x-5)")
plt.plot(x,y3,label = "y = sin(x)")
plt.plot(x,y4,label = "y = cos(x) * sin(x)")
plt.legend()

plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Function Image : f(x) = cos(x)//f(x) = cos(x) * sin(x)")
plt.grid()
plt.show()

student2023033 LV 3 @ 2024-12-13 18:35:16

已修改

使用运动方程表现理想情况下和实际实验中的球运动轨迹的对比。

“在理想情况下，各种阻力都小到可以忽略不计，小球将会沿右侧斜面上升到与左侧下落点等高的地方。右侧斜面的坡度越小，小球要上升到相同高度所用的时间就越长，运动路程也越远。如果右侧斜面平放成水平面，那么，小球因为永远无法达到那个高度将一直运动下去。”

——摘自义务教育教科书•物理•八年级•全一册•上海科学技术出版社P162

绘制伽利略思想实验中球运动轨迹

定义域与参数范围:

定义域: ( 0 \leq x \leq 10 )（表示时间，秒）
对于理想情况下的运动（无能量损失）：
- 初始高度 ( h_0 = 10 ) 米
- 重力加速度 ( g = 9.8 , \text{m/s}^2 )
- 运动方程: ( h(t) = h_0 - \frac{1}{2} g t^2 )

对比函数:

实际实验中，由于空气阻力、摩擦力等因素的影响，球的高度会逐渐降低，最终停止。
模拟实际实验的运动方程: ( h'(t) = h_0 - \frac{1}{2} g t^2 - k t )（其中 ( k ) 为阻尼系数）

绘制的函数图像

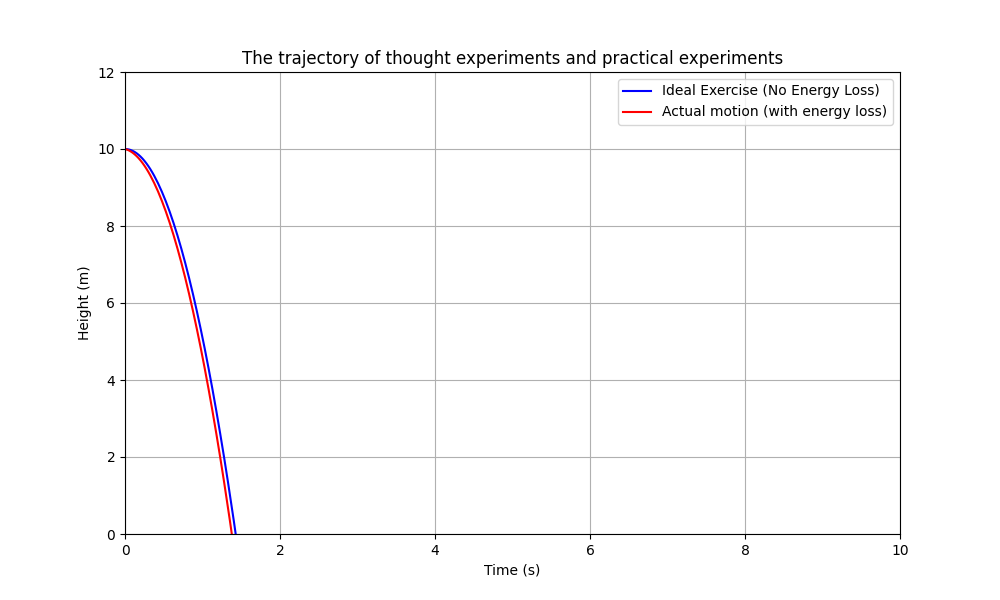
Function Image: Ideal vs. Real Motion

我的观察与思考

理想情况下的运动:
- 球从 10 米的高度自由落下，按照 ( h(t) = 10 - \frac{1}{2} \cdot 9.8 \cdot t^2 ) 的规律运动。
- 图像为一个开口向下的抛物线，表示球在理想情况下会一直运动，直到与起始高度相同的高度（如果无坡，则会一直运动）。
- 在 ( t = 1.43 ) 秒时，球达到最高点（10 米），然后开始下落。
实际实验中的运动:
- 由于空气阻力、摩擦力等因素的影响，球的高度逐渐降低，最终停止。
- 模拟实际实验的运动方程为 ( h'(t) = 10 - \frac{1}{2} \cdot 9.8 \cdot t^2 - 0.5 \cdot t )（假设阻尼系数 ( k = 0.5 )）。
- 图像为一个逐渐下降的曲线，表示球在运动过程中逐渐失去能量，最终停止。
对比:
- 理想情况下的运动曲线对称于最高点，而实际实验中的运动曲线逐渐下降。
- 理想情况下，球会一直运动到与起始高度相同的高度，而实际实验中，球最终会停止在某个较低的高度。

代码

import matplotlib.pyplot as plt
import numpy as np

# 创建时间点
t = np.linspace(0, 10, 400)  # 从0到10秒之间生成400个点

# 定义理想情况下的运动方程 h(t) = h0 - 0.5 * g * t^2
g = 9.8  # 重力加速度 (m/s^2)
h0 = 10  # 初始高度 (m)
h_ideal = h0 - 0.5 * g * t**2

# 定义实际实验中的运动方程 h'(t) = h0 - 0.5 * g * t^2 - k * t
k = 0.5  # 阻尼系数 (m/s)
h_real = h0 - 0.5 * g * t**2 - k * t

# 绘制图像
plt.figure(figsize=(10, 6))
plt.plot(t, h_ideal, label='Ideal Exercise (No Energy Loss)', color='blue')
plt.plot(t, h_real, label='Actual motion (with energy loss)', color='red')

plt.xlabel('Time (s)')  # x轴标签
plt.ylabel('Height (m)')  # y轴标签
plt.title('The trajectory of thought experiments and practical experiments')  # 图像标题
plt.legend()  # 显示图例
plt.grid()  # 显示网格
plt.axhline(0, color='black', linewidth=0.5)  # x轴
plt.axvline(0, color='black', linewidth=0.5)  # y轴
plt.xlim(0, 10)  # 设置x轴范围
plt.ylim(0, 12)  # 设置y轴范围
plt.show()  # 显示图像

student2023028 LV 2 @ 2024-12-13 18:35:14

已修改

绘制y=x^n的图像，观察其中变化规律。

1.定义域-1<=x<=1,n的值2到4到8到16变化。

2.绘制的函数图像如下图：

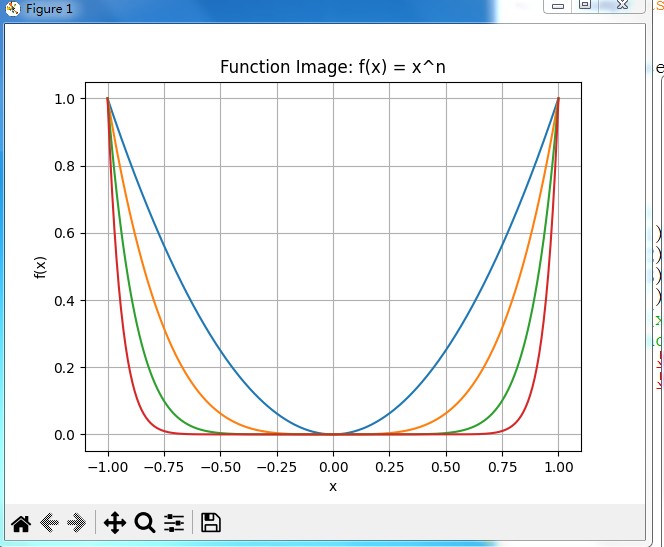
3.我的观察与思考：这张图展示了函数f(x) = x^n的图像

对称性

1. 当n为偶数时（例如n = 2, 4, 6\cdots）

函数y = x^{2k}（k为正整数）是偶函数。
偶函数的特点是关于y轴对称，即f(x)=f( - x)。从图中可以看到，蓝色和绿色曲线（可能对应偶数n值）在y轴两侧是对称的。 2. 当n为奇数时（例如n = 1, 3, 5\cdots）
函数y=x^{2k + 1}（k为非负整数）是奇函数。
奇函数的特点是关于原点对称，即f(-x)=-f(x)。图中的红色和黄色曲线（可能对应奇数n值）在原点两侧是对称的。

单一性

1. 当n为偶数时

函数y = x^{2k}在x\geq0时单调递增，在x<0时单调递减。
从图中可以看到，蓝色和绿色曲线在x = 0处有最小值0，并且在x>0时曲线上升，在x<0时曲线下降。 2. 当n为奇数时
函数y=x^{2k + 1}在整个定义域(-\infty,\infty)上单调递增。
图中的红色和黄色曲线从左到右是持续上升的，没有下降的部分。

3.绘制的函数的代码：

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-1, 1, 400)  # 从-1到1之间生成400个点
y=x**2
y1=x**4
y2=x**8
y3=x**16

# 绘制图像
plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = x^n')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023025 LV 5 @ 2024-12-13 18:33:26

已修改

绘制y=sin(x+n)的图像，观察其中变化规律。

1.定义域-1<=x<=1,n的值1到1.5到2到2.5到3到3.5变化。

2.绘制的函数图像如下图：

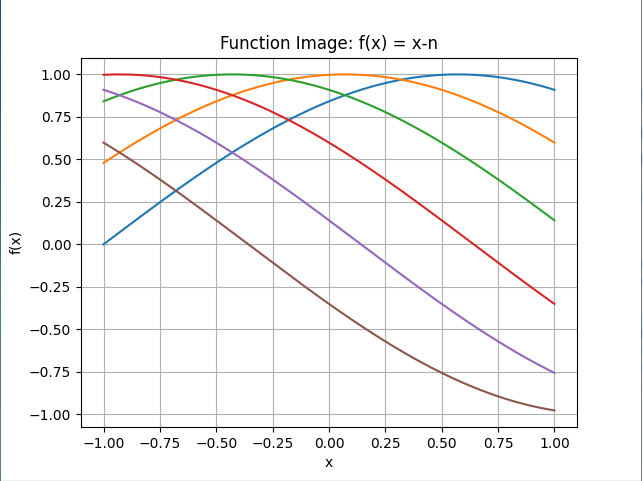
3.我的观察与思考：

对称性：它依然保留了正弦函数的对称特性。图像绕这些点旋转后180d°能与自身重合

周期性：从图像上可以看出，它的图像呈波浪状不断重复出现，其最小正周期依然是2Π。通过观察图像上相邻波峰或者波谷之间的水平距离，就能直观确定这一周期特性。

值域范围：函数的值域保持不变，依旧是（-1，1）。从图像上来看，图像始终在y=-1和y=1这两条水平直线所夹的区域内波动，无论如何取值，对应的函数值都不会超出这个区间。 4.绘制的函数的代码：

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-1, 1, 400)  # 从-10到10之间生成400个点
y = np.sin(x+1)
y1 =np.sin(x+1.5)
y2 =np.sin(x+2)
y3 =np.sin(x+2.5)
y4 =np.sin(x+3)
y5 =np.sin(x+3.5)

# 绘制图像
plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y4)
plt.plot(x, y5)
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = x-n')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

student2023011 LV 3 @ 2024-12-13 18:33:19

1'函数：y=sin(x+2) y=sin(x+4) y=sin(x+8) x的范围:-20<x<20

2'截取绘制函数的图像

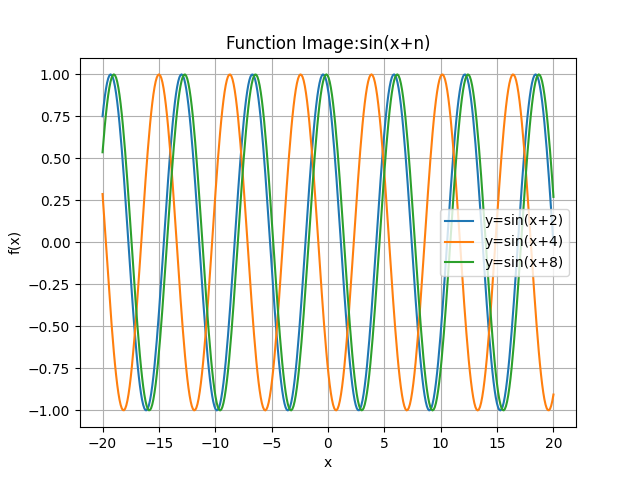
3'我的思考与发现：

x加的值越大在图中的起始位置越靠右，并且三个函数的最大y坐标和最小y坐标相等，三组函数十分对称

4'代码


import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(-20,20,400)
y1=np.sin(x+2)
y2=np.sin(x+4)
y3=np.sin(x+8)

plt.plot(x,y1,label='y=sin(x+2)')
plt.plot(x,y2,label='y=sin(x+4)')
plt.plot(x,y3,label='y=sin(x+8)')
plt.legend()

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Function Image:sin(x+n)')
plt.grid()
plt.show()

student2023048 LV 1 @ 2024-12-13 18:32:58

已修改

1.说明要绘制的函数，以及定义域x的范围。分别是y=sin(x)和y=sin(2x);定义域x的范围是从0到4π。这里使用了np.linspace函数生成了1000个点，用于后续绘制函数图像时作为横坐标的值。 2.截取绘制函数的图像。 见最底

3.说明你对函数图像的观察与思考。从绘制出的图像来看，绿色的曲线相对 “平缓” 一些，波动节奏慢，而粉色的曲线波动更为密集、快速，二者相互交织，通过图像可以很直观地对比出它们在周期、变化频率等方面的差异

4.提供绘制函数图像的代码。

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 4 * np.pi, 1000)  

y1 = np.sin(x)
y2 = np.sin(2 * x)

plt.figure(figsize=(10, 6)) 

plt.plot(x, y1, label=r'$y = \sin(x)$', color='green', linewidth=2)

plt.plot(x, y2, label=r'$y = \sin(2x)$', color='pink', linewidth=2)

plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.title('$y = \sin(x)$ and $y = \sin(2x)$', fontsize=16)

plt.legend(fontsize=12)

plt.grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()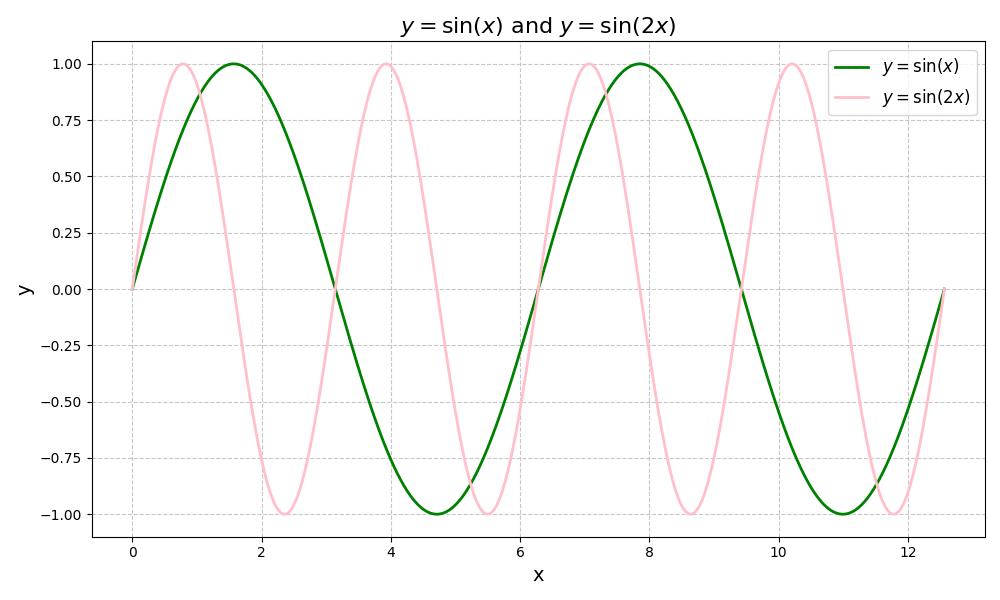

QiHong SU @ 2024-11-8 17:58:13

已修改

绘制y=x^n的图像，观察其中变化规律。

1.定义域-1<=x<=1,n的值0到1到2到3到5到10变化。

2.绘制的函数图像如下图：

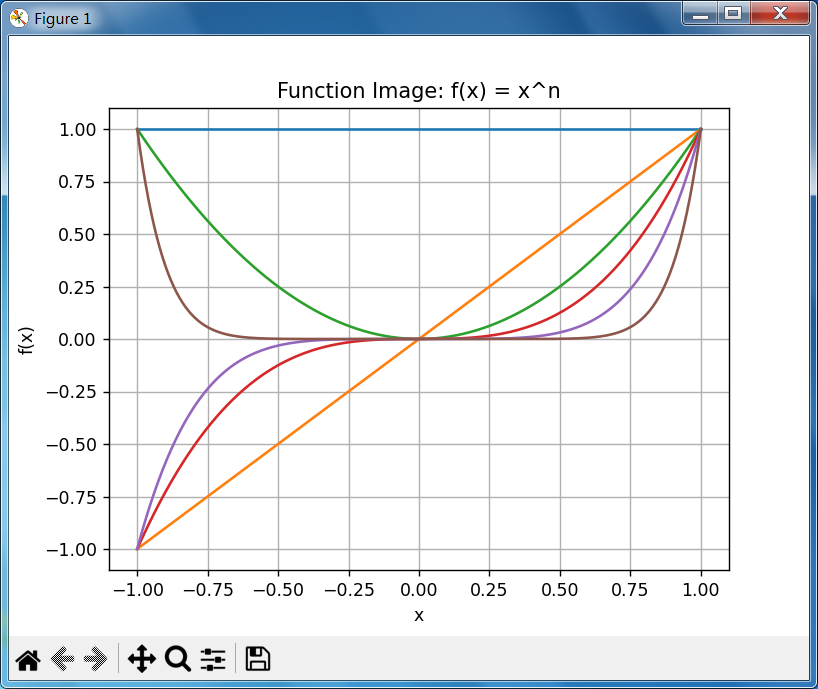
3.我的观察与思考：

对称性：当n为偶数时，函数的图像y=x^n关于y轴对称，是偶函数；当n为奇数时，函数图像关于原点对称，是奇函数。

过点情况：所有函数都过点(-1,1)，(0,0)，(1,1) 。

单调性：当n为奇数时，在-1到1之间函数单调递增；当为偶数时，在-1到0之间函数单调递减，在0到1之间函数单调递增。

增长速度：随着n的增大，当x的绝对值大于0且小于1时，函数值的变化速度越来越快，即图像在x=0附近越来越陡峭。

3.绘制的函数的代码：

import matplotlib.pyplot as plt
import numpy as np

# 创建数据点
x = np.linspace(-1, 1, 400)  # 从-10到10之间生成400个点
y = x**0
y1 = x**1
y2 = x**2
y3 = x**3
y5 = x**5
y10 = x**10

# 绘制图像
plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y5)
plt.plot(x, y10)
plt.xlabel('x')  # x轴标签
plt.ylabel('f(x)')  # y轴标签
plt.title('Function Image: f(x) = x^n')  # 图像标题
plt.grid()  # 显示网格
plt.show()  # 显示图像

‌

👍 6

❤️ 3

👎 2

student2023003 LV 1 @ 2024-12-13 18:43:15

绘制y=x^n的图像，观察其中变化规律。

1.定义域-5<=x<=2,n的值0到1到2到3到5到10变化。

2.绘制的函数图像如下图：

3.我的观察与思考：两条不相交的直线但越到后面就会相交，一种增长性的体现

3.绘制的函数的代码：

import matplotlib.pyplot as plt import numpy as np #创建数据点 x=np.linspace(-5,-2,100)#从-2到-2中取100个点

y = x0 y1 = x1 y2 = x2 y3 = x3 y5 = x5 y10 = x10 #绘制图像 plt.plot(x,y1, label='y=sin(x)') plt.plot(x,y2, label='y=sin(x+5)') plt.plot(x,y1, label='y=5sin(x)') plt.legend()#添加图例显示每条线段对应点 plt.xlabel('x')#x轴标签 plt.ylabel('fx')#y轴标签 plt.title('Function Image: f(x)=sin(x)') plt.grid()#显示网格 plt.show()#显示图像

基本数学函数f(x)图像绘制

45 条评论

1.说明要绘制的函数，以及定义域x的范围:

2.截取绘制函数的图像。

4.提供绘制函数图像的代码:

1.绘制的函数

2.函数的图像

3.观察与思考

4.图像的代码

函数：

定义域：

截取绘制函数的图像:

代码

1.绘制三次函数这里示例为y = x^3，所以a = 1, b = 0, c = 0, d = 0

2.截取绘制函数的图像。

3.说明你对函数图像的观察与思考。

1. 说明要绘制的函数，以及定义域x的范围。

函数：y=cos(k) * sin(k * x)

定义域：x 可以取任意的实数

2.截取绘制函数的图像。

3.说明你对函数图像的观察与思考。

组成结构

对称轴

特殊点

4.提供绘制函数图像的代码。

一、 函数、定义域说明

二、 函数图像截图

三、 对函数图像的观察与思考

单调性：

形状特点：

四、 绘制函数图像的代码

1、x 的范围是从 -10 到 10，一共生成 400 个等间隔的值。

2、函数图像：

3、观察：首先，用代码画函数图像很神奇，只要改一下函数定义就能画出不同的图像。而且还能调整图像的范围和精细程度。图像上有坐标轴标签、标题和网格线，看起来很清楚。这个方法能画很多种数学函数的图像呢。

4、代码：

1.要绘制的函数以及定义域x的范围：

2.截取绘制函数的图像：

3.你对函数图像的观察与思考：

4.绘制函数图像的代码：

1.说明要绘制的函数，以及定义域x的范围。

2.截取绘制函数的图像。

3.说明你对函数图像的观察与思考。

4.提供绘制函数图像的代码。

图像截图：

代码：

绘制f(x)=2x^3的图像，观察其中变化规律。

定义域-10<=x<=10(n为整数)

绘制的函数图像如下图：

我的观察与思考：

绘制y=nx+(n-1)/x（对勾函数）的图像，观察其中的规律

1.绘制的函数：

2.图片：

3.思考：

4.代码：

1和2.说明要绘制的函数，以及定义域x的范围。

截取绘制函数的图像。

3.说明你对函数图像的观察与思考。

4.提供绘制函数图像的代码。

绘制伽利略思想实验中球运动轨迹

绘制的函数图像

我的观察与思考

代码

状态

开发

支持

登录

函数：**y=cos(k) * sin(k * x)**

一、函数、定义域说明

二、函数图像截图

三、对函数图像的观察与思考

四、绘制函数图像的代码