- Turtle创作分享
Turtle创作数字规律图像-2026届科技班
- @ 2024-11-10 10:36:53
1.说明设计数字规律与作品变化主要特征。
2.截取作品的图像放在下面。
3.提供作品绘制的代码。
50 条评论
-
 student2023043 @ 2024-11-10 17:20:06
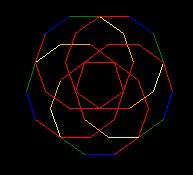
student2023043 @ 2024-11-10 17:20:06线段变化长短加上旋转绘成图形
import turtle as t t.speed(0.1) m=0 t.pensize(2) x=int(input()) c=360/x d=1 for i in range(150): m=m+1 t.fd(d) t.left(c+2) d=d+3 if m%6==0: t.pencolor("blue") elif m%6==1: t.pencolor("red") elif m%6==2: t.pencolor("purple") elif m%6==3: t.pencolor("yellow") elif m%6==4: t.pencolor("green") else: t.pencolor("brown")当x=4时
 当x=6时
当x=6时 👍 1😄 1❤️ 1👎 1
👍 1😄 1❤️ 1👎 1 -
 @ 2024-11-10 16:56:50
@ 2024-11-10 16:56:501.规律:画出N条枝条的雪花 2.图像截图 n=6
 n=5
3.代码
n=5
3.代码import turtle as t t.bgcolor("blue") t.color("white") t.pensize(5) t.speed(0) def x(a,b): t.fd(a) t.bk(a) t.lt(22.5) t.fd(b) t.bk(b) t.rt(45) t.fd(b) t.bk(b) t.lt(22.5) n=int(input()) m=360/n if m<=90: z=90-m else: z=m-90 t.lt(z) for i in range(n): t.fd(100) x(100,100) t.lt(22.5) for i in range(2): t.fd(40) x(40,25) t.bk(80) t.rt(45) for i in range(2): t.fd(40) x(40,25) t.bk(80) t.lt(22.5) t.fd(100) x(100,100) t.lt(22.5) for i in range(2): t.fd(60) x(60,50) t.bk(120) t.rt(45) for i in range(2): t.fd(60) x(60,50) t.bk(120) t.lt(22.5) t.fd(100) x(30,50) t.fd(30) x(30,25) t.bk(330) t.lt(m) t.rt(m*1/2) for i in range(n): t.fd(75) x(75,60) t.fd(75) x(75,60) t.bk(150) t.lt(m) t.done()👍 1 -
 @ 2024-11-10 16:52:26
@ 2024-11-10 16:52:26
```import turtle as t x=8 t.pensize(2) colors = ["red","purple","yellow","blue","pink","green","black","orange"] t.speed(0) while x<350: t.pencolor(colors[x%8]) t.forward(x) t.left(360/8) x=x+1 t.done()👎 3👍 1 -
@ 2024-11-10 16:52:23
1.代码
import turtle turtle.setup(800, 600) turtle.bgcolor("black") pen = turtle.Turtle() pen.speed(10) pen.color("pink") def draw_petal(): for i in range(11): if i/10 == 0.9: pen.color("red") elif i/10 == 0.8: pen.color("orange") elif i/10 == 0.7: pen.color("yellow") elif i/10 == 0.6: pen.color("green") elif i/10 == 0.5: pen.color("blue") pen.forward(30) pen.right(36) for _ in range(10): draw_petal() pen.right(36) pen.hideturtle() turtle.done()2.图片:
 👎 2👍 1
👎 2👍 1 -
 @ 2024-11-10 16:52:22
@ 2024-11-10 16:52:22import turtle import random turtle.setup(800, 600) turtle_obj=turtle.Turtle() turtle_obj.speed(0) turtle_obj.penup() colors=["#0000FF", "#0000CC", "#000099", "#000066", "#000033", "#000000"] def draw_triple_spiral(x, y, size): turtle_obj.goto(x, y) turtle_obj.pendown() for color in colors: turtle_obj.pencolor(color) for _ in range(3): turtle_obj.forward(size) turtle_obj.right(120) size -= 2 turtle_obj.penup() for _ in range(300): x = random.randint(-400, 400) y = random.randint(-300, 300) size = random.randint(50, 150) draw_triple_spiral(x, y, size) turtle_obj.hideturtle() turtle.done() 👎 1
👎 1 -
 @ 2024-11-10 16:50:54
@ 2024-11-10 16:50:541.(根据齐老师绘制正n边形修改)规律:在每一次绘制中,由上一次画笔经左转 60 度、前进50、左转 60 度、前进50的操作变换得到。
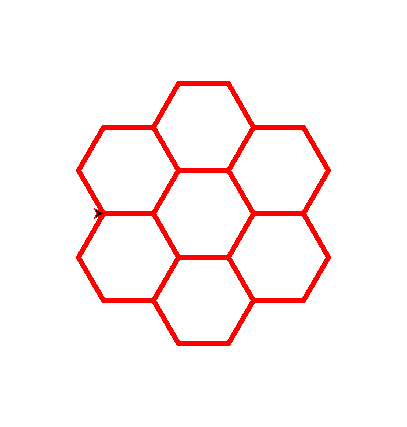
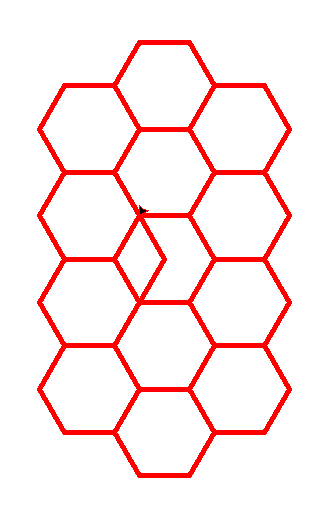
 3.
3.import turtle turtle.pensize(5) turtle.pencolor('red') turtle.tracer (n=20,delay=10) for i in range(4): for i in range(3): for i in range(6): turtle.forward(50) turtle.left(360/6) turtle.forward(50) turtle.right(60) for i in range(6): turtle.forward(50) turtle.left(360/6) turtle.forward(50) turtle.right(60) turtle.left(60) turtle.forward(50) turtle.left(60) turtle.forward(50) turtle.done()👍 2👎 2 -
 @ 2024-11-10 16:47:23
@ 2024-11-10 16:47:231:线段变化长短加上旋转绘成图形
import turtle a = turtle turtle.tracer(0) a.bgcolor('black') sides=2 colors=['white','yellow'] for x in range(340): a.color(colors[x%sides]) a.forward(x*2/sides+x) a.left(340/sides+1) a.left(70)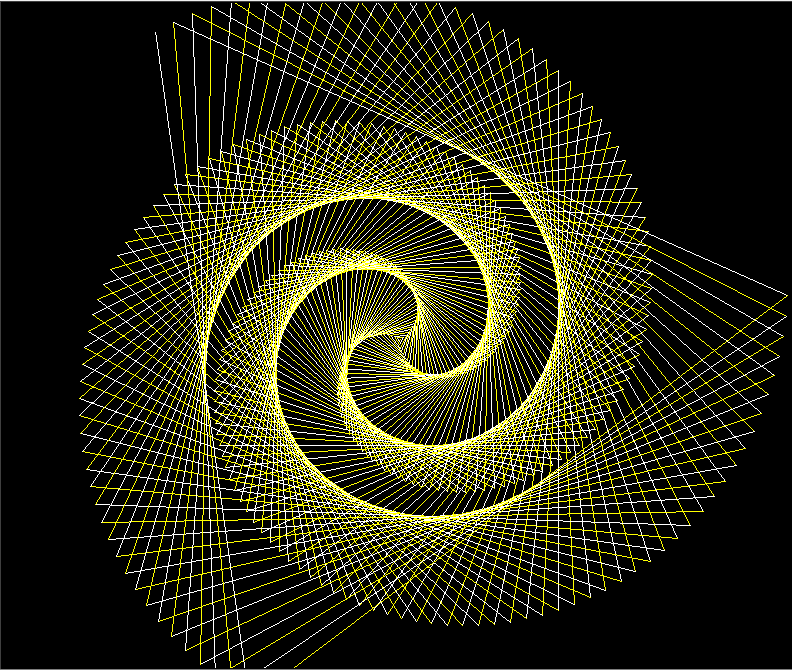 👍 3❤️ 1👎 1
👍 3❤️ 1👎 1 -
 @ 2024-11-10 16:46:51
@ 2024-11-10 16:46:51
 1.正方形旋转变化
1.正方形旋转变化2.代码:
import turtle t = turtle.Pen() turtle.bgcolor("black") sides=6 colors=["pink","yellow","pink","white","orange","white"] for x in range(340): t.pencolor(colors[x%sides]) t.forward(x*2/sides+x) t.left(540/sides+1) t.width(x*sides/100) print ```👍 1👎 1 -
@ 2024-11-10 16:45:47
import turtle as t t.speed(0) n=int(input()) for i in range(int(n)): for i in range(int(n+(n/2))): t.fd(100) t.left(360/n) t.left(360/(n/2))1..说明设计数字规律与作品变化主要特征: 画n个首尾相接的正n边型 3.
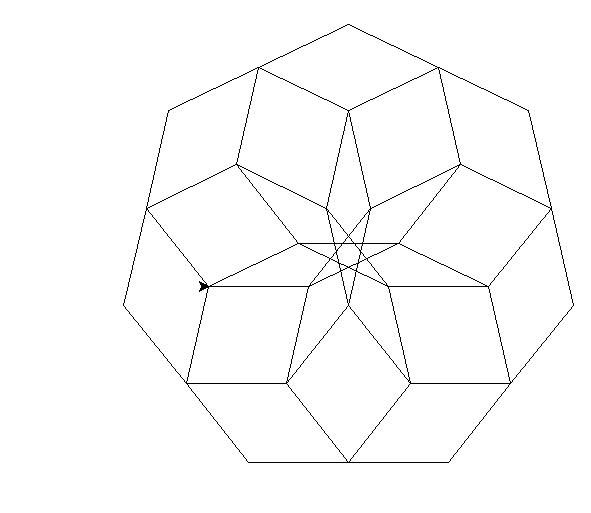 👍 2👎 1
👍 2👎 1 -
 @ 2024-11-10 16:40:24
@ 2024-11-10 16:40:241.绘制角度变化的图形
2.成品图片(输入不同的数据,所呈现的效果也可能会不同)
当输入10时的效果:

当输入50时的效果:
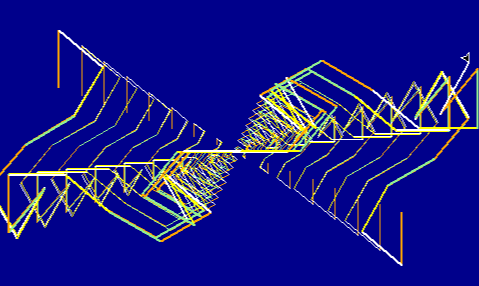
当输入100时的效果:

3.代码
import turtle as t m = 1 x=5 s = 1 n = int(input("旋转角度:")) a = n t.bgcolor("dark blue") t.speed(0) t.pensize(s) colors = ["yellow","light green","orange","white"] for i in range(2000): t.pencolor(colors[i%4]) t.forward(m) t.left(a) x+=1 a+=n m += 0.1 s+=0.001 t.pensize(s) t.done()👍 3👎 2 -
 @ 2024-11-10 16:35:56
@ 2024-11-10 16:35:561.双色自定义边数间距循环图 2.截图 边数:3;间距:1
 边数:3;间距:2
边数:3;间距:2
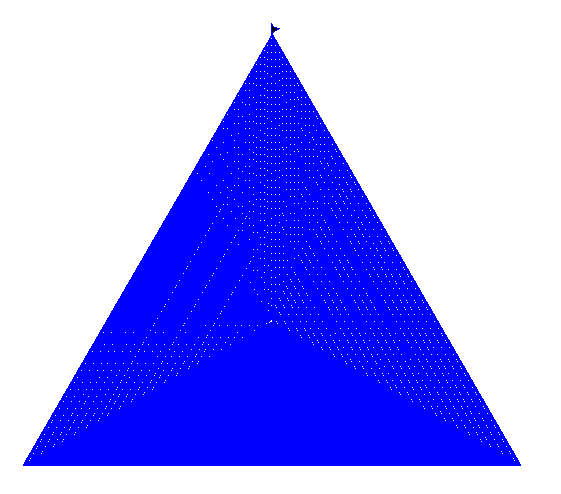 边数:4;间距:1
边数:4;间距:1

import turtle as t x=5 t.pensize(2) colors = ["purple","blue"] t.speed(0) n=int(input("请输入设计图案的边数:")) a=360/n v=int(input("请输入设计图案的间距:")) while x<500: t.pencolor(colors[x%2]) t.forward(x) t.left(a) x=x+v t.done()👍 3❤️ 1👎 1 -
 @ 2024-11-10 16:34:23
@ 2024-11-10 16:34:231.图案设计思考: 如何体现图案的规律?如何增强体验性? 2.绘制的图像:

3.绘制代码:
import turtle as t t.pensize(3) t.screensize(500,300) cl = [ "red","yellow","blue","green","red","pink"] t.speed (0) t.pencolor("red") n=int(input("输入次数:(最好大于一百)")) b=int(input("输入角度:")) a = 7 for i in range(n): cl1 = cl[i%6] t.pencolor(cl1) t.fd(a) t.left(b) a = i + 7 t.down t.listen() t.mainloop()👍 4👎 2 -
 @ 2024-11-10 16:34:19
@ 2024-11-10 16:34:191.在每次画完一朵花瓣后旋转90度画下一朵花瓣
2.
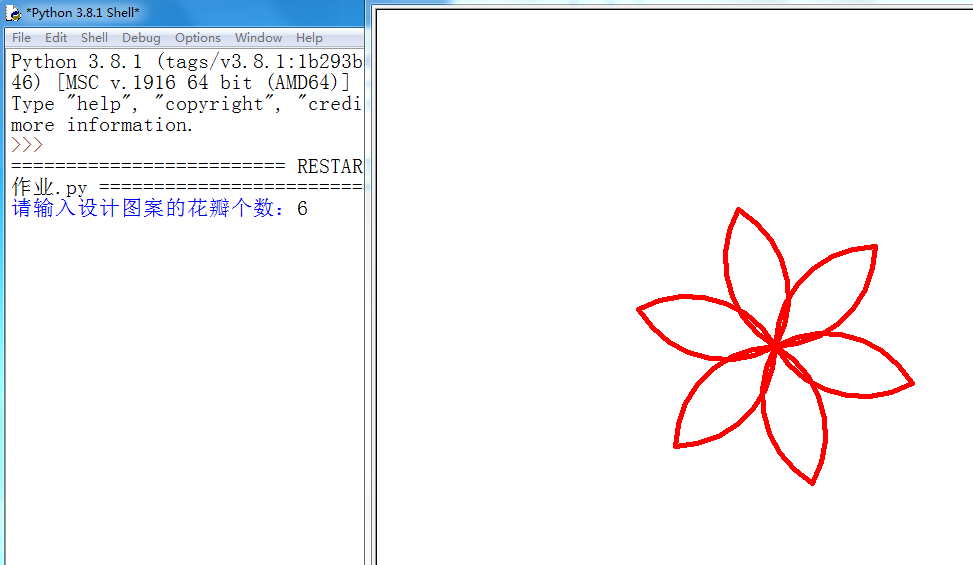
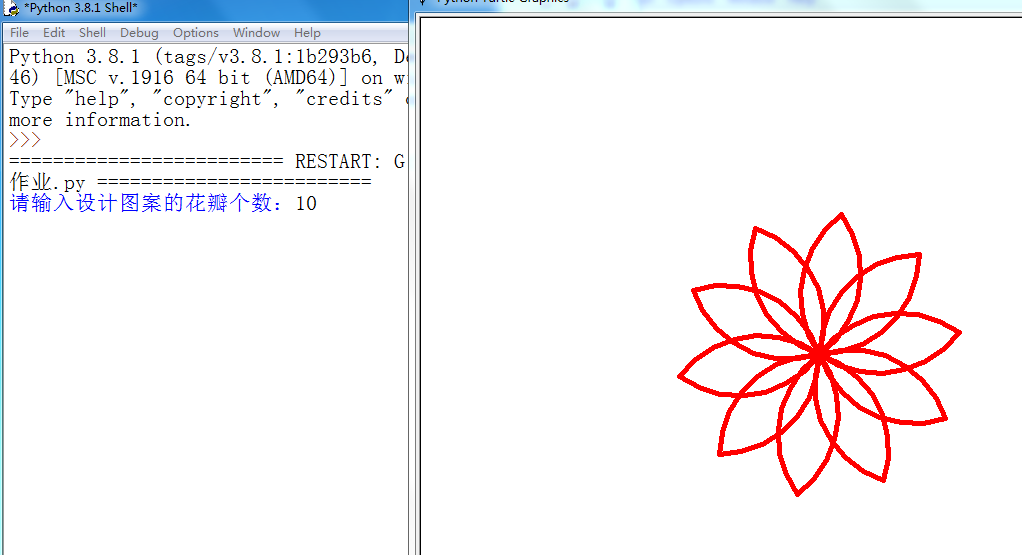
3.代码:
```import turtle as t t.pencolor("red") t.pensize(5) t.speed(0) def draw_petal(a,b): t.circle(a,b) t.left(90) t.circle(a,b) t.left(90) n=int(input("请输入设计图案的花瓣个数:")) a=360/n for _ in range(n): draw_petal(100,90) t.right(a) t.hideturtle() t.done()👍 3👎 1 -
 @ 2024-11-10 16:32:45
@ 2024-11-10 16:32:45绘制旋转的圆圈图案
1.图案设计思考:
设计绘制的图案如何让颜色随机,让圆圈代替多边形,旋转?
2.绘制的图像:


3.绘制的代码:
import turtle import math screen = turtle.Screen() screen.bgcolor("black") screen.title("旋转的圆圈图案") pen = turtle.Turtle() pen.speed(0) pen.width(2) pen.hideturtle() colors = ["red", "orange", "yellow", "green", "blue", "indigo", "violet"] # 定义颜色列表 num_circles = 10 initial_radius = 100 rotation_speed = 2 angle = 0 # 初始化角度为0度 while angle < 360 * rotation_speed: for i in range(num_circles): # 循环绘制每一层圆圈 radius = initial_radius + i * 20 x = radius * math.cos(math.radians(angle)) # x坐标 y = radius * math.sin(math.radians(angle)) # y坐标 pen.penup() # 抬 pen.goto(x, y) # 移 pen.pendown() # 放 pen.color(colors[angle % len(colors)]) # 选 pen.circle(50) # 绘半径50圆 angle += 5 # 加5度 # keep turtle.done() draw_multiple_rotating_circles(num_circles, radius, rotation_speed) #keep turtle.done()👍 8🌿 7😕 6😄 6👀 6🍋 4🤡 4🕊️ 4👎 1 -
 @ 2024-11-10 16:32:26
@ 2024-11-10 16:32:261.图案设计思考: 设计由不断旋转的规则图形组成的图案,需要输入角度(不同角度能形成不同规则图形) 2.绘制的图像: 198度:
 88度:
88度:

3.绘制的代码:
import turtle as t t.pensize(3) cl = [ "red","yellow","blue","green","red","pink"] cl2 = ["red","white","red","white","red","white"] t.speed (0) t.pencolor("red") x = int (input("请输入旋转角度(建议不小于30):")) a = 7 for i in range(2024) : cl1 = cl[i%6] t.pencolor(cl1) t.fd(a) t.left(x) a = i + 7 t.down t.mainloop()👍 4👎 1 -
@ 2024-11-10 16:31:03
创作规律环形 1.图案设计思考:画笔每走一步,就变化走的距离,在变化粗细,颜色等,重复起来,会发生什么?
2.绘制的图像: (1)重复200次
 (2)重复1100次
(2)重复1100次

2.绘制的代码:
import turtle as tu print("请输入重复次数(470~1100):") x=input() q=0.1 z=0.01 y=20 q=int(q) z=int(z) x=int(x) tu.pencolor("red") tu.speed(0) colors = ["red","purple","yellow","blue","brown","black","green"] for i in range(x): tu.forward(z) tu.right(5) tu.pensize(q) tu.pencolor(colors[y%7]) z=z+0.1 q=q+0.1 y=y+5👍 3👎 1 -
 @ 2024-11-10 16:29:19
@ 2024-11-10 16:29:191.图案设计思考: 不同的角度能绘制出不同的图形 2绘制的图案(输入6):
 3.绘制的代码:
3.绘制的代码:import turtle as t x=5 n=int(input()) t.pensize(1) colors = ["green","blue","brown"] t.speed(0) while x<1000: t.forward(x) t.pencolor(colors[x%3]) t.left(((n-2)*180/n)+50) x=x+5 t.done()👍 1👎 1 -
@ 2024-11-10 16:26:42
这是一个能绘制螺旋线的程序。用户可以决定螺旋线的条数和每条螺旋线的颜色。
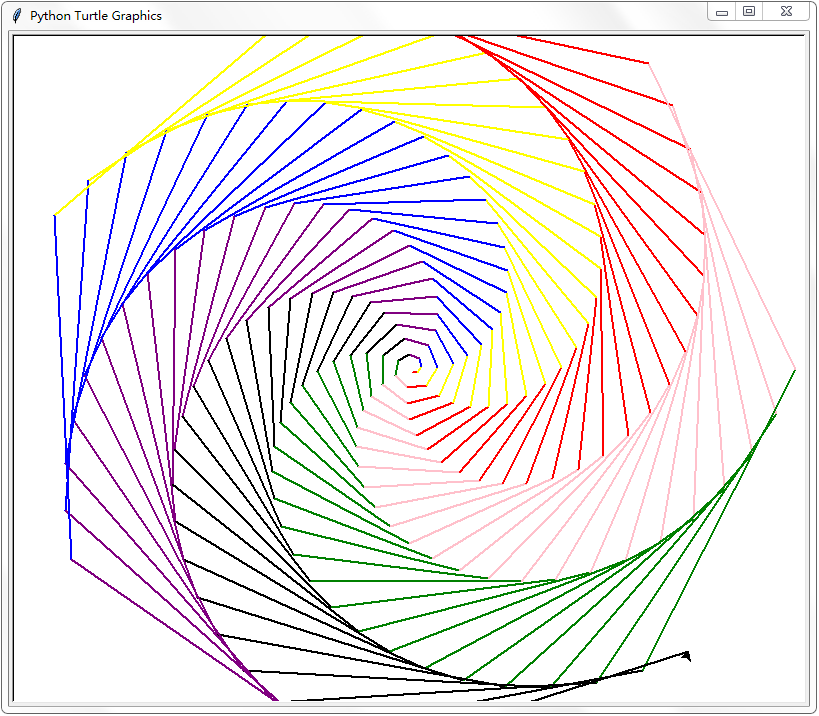
```import turtle as t x=5 t.pensize(2) colors = [] t.speed(0) print("请输入螺旋线的条数:") m=int(input()) y=360/m print("请分别输入",m,"种颜色:") for i in range(m): f=input() colors.append(f) d=0 while x<350: t.pencolor(colors[d%m]) d=d+1 t.forward(x) t.left(y+1) x=x+2 t.done()👍 5👎 1 -
 @ 2024-11-10 16:25:36
@ 2024-11-10 16:25:361.以圆形为基础,不断改变其颜色和粗细
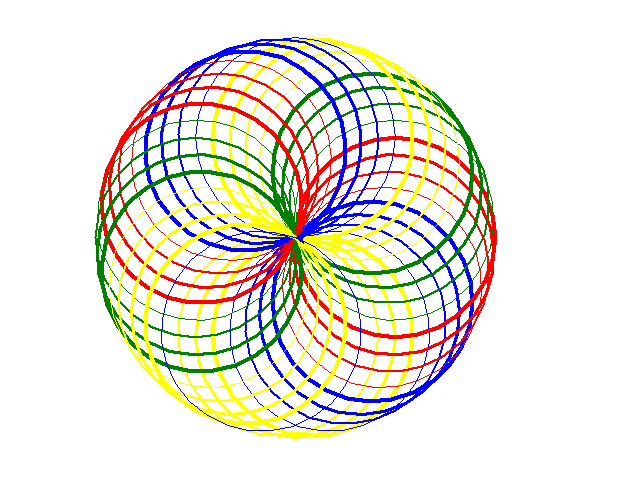
import turtle as t t.reset() t.speed(0) for i in range(0,360,10): for c in ('blue', 'red', 'green','yellow'): for a in (1,2,3,4): t.color(c) t.pensize(a) t.circle(100) t.left(10)👍 2👎 1 -
 @ 2024-11-10 16:25:16
@ 2024-11-10 16:25:161.(根据齐老师四边形边长递增代码修改)将原有的while判断循环次数并推出循环改为if-break语句,新增用户输入一个数字以用户输入的数字为n边形边数并画出相应图案 2.代码截图(以五边形为例)
 3.代码
3.代码# 绘制边长递增的n边形 import turtle as l u=int(input()) l.pensize(2) l.pencolor("red") o=5 while True: for _ in range(u):#新增for结构 l.forward(o) l.left(360/u) o+=5 if o>500:#改用if-break语句判断是否结束 break l.done() #原代码为齐老师的,我对结构进行了一定调整并增加用户输入边数输出对应图形的功能👎 2👍 1 -
 @ 2024-11-10 16:24:49
@ 2024-11-10 16:24:491.图形由不同的图形环绕而成,可以控制图形边数及循环次数 2.
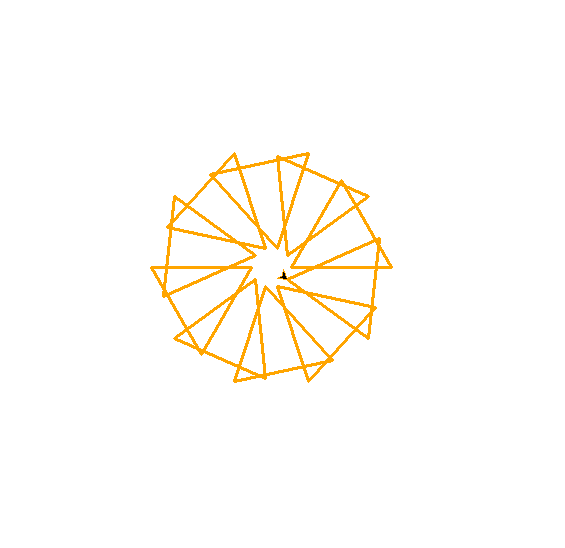

3.代码
import turtle as t import math t.pensize(3) colors = ["red","orange","yellow","green","blue","purple"] g=7 t.speed(0) def draw(a,b,c): angle_between = 360 / b for i in range(b): t.penup() t.pencolor(colors[g%6]) t.goto(0, 0) t.setheading(angle_between * i) t.forward(c) t.pendown() for e in range(a): t.forward(100) t.left(360 / a) n=int(input("请输入设计图案(单个)的边数:")) m=int(input("请输入设计图案循环的次数:")) h=int(input("请输入设计图案半径:")) a=n b=m c=h draw(a,b,c) t.done()👎 2👍 1 -
 @ 2024-11-10 16:23:52
@ 2024-11-10 16:23:521.旋转角度缓缓变大 2.

3
import turtle a=int(input("请输入正多边形的边数: ")) b=turtle.Turtle() c=50 d=5 b.speed(100) b.pencolor("cyan") turtle.bgcolor("black") for i in range(100): for j in range(a): b.forward(c) b.right(360/a) c+=2 b.right(d) turtle.done()👍 3👎 1🤔 1🍋 1👀 1🤡 1😕 1🌿 1😄 1❤️ 1 -
 @ 2024-11-10 16:23:45
@ 2024-11-10 16:23:45规律:
在每一层级绘制中,由上一层级曲线经右转 90 度、绘制上一层级曲线、左转 90 度的操作变换得到,同时,右转和左转 90 度的转向规律决定曲线弯曲方向。
代码:
import turtle turtle.screensize(bg="black") turtle.pencolor("white") turtle.hideturtle() turtle.speed(0) def draw_dragon_curve(level, len): if level == 0: turtle.forward(len) return draw_dragon_curve(level - 1, len) turtle.right(90) draw_dragon_curve(level - 1, len) turtle.left(90) n=int(input("重复的次数(n<=1000):")) m=int(input("线段的长度")) draw_dragon_curve(n, m) turtle.done()图片:

给不同大小的参数会有不同的效果!(画得有点慢...)
👍 8👎 6❤️ 4😄 4👀 4😕 3🌿 3🤔 1 -
 @ 2024-11-10 16:23:33
@ 2024-11-10 16:23:33- 数字规律: 分形树。 缩放因子: 0.6375, 比例缩放规律。
- 图片
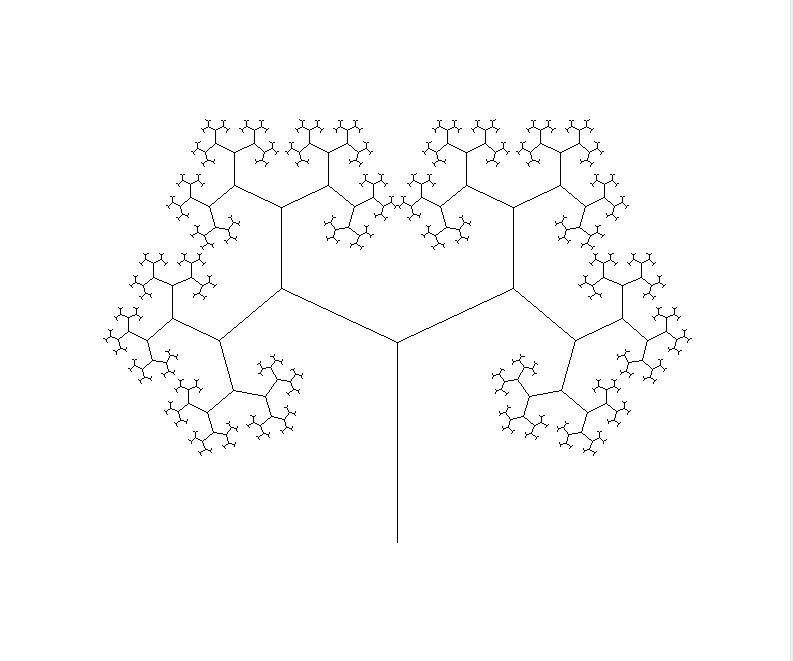
- 代码
import turtle def a_(plist, l, a, f): if l > 3: lst = [] for p in plist: p.forward(l) q = p.clone() p.left(a) q.right(a) lst.append(p) lst.append(q) for x in a_(lst, l*f, a, f): yield None def m(): p = turtle.Turtle() p.setundobuffer(None) p.hideturtle() p.speed(0) p.getscreen().tracer(30,0) p.left(90) p.penup() p.forward(-210) p.pendown() t = a_([p], 200, 65, 0.6375) for x in t: pass m()👍 5👎 4 -
 @ 2024-11-10 16:22:16
@ 2024-11-10 16:22:161该图案是以3种颜色的花瓣旋转组成

import turtle as t t.pensize(5) t.speed(0) c=["yellow","#a0c8f0","pink"] for _ in range(24): t.pencolor(c[_%3]) t.circle(80, 120) t.right(-45) t.circle(70, 120) t.right(165) t.right(-45) draw_flower() t.done()👍 5👀 3🌿 3❤️ 3😄 3😕 3🕊️ 3👎 2 -
 @ 2024-11-10 16:20:23
@ 2024-11-10 16:20:23阿基米德螺线 1思考 探究一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹 2图像
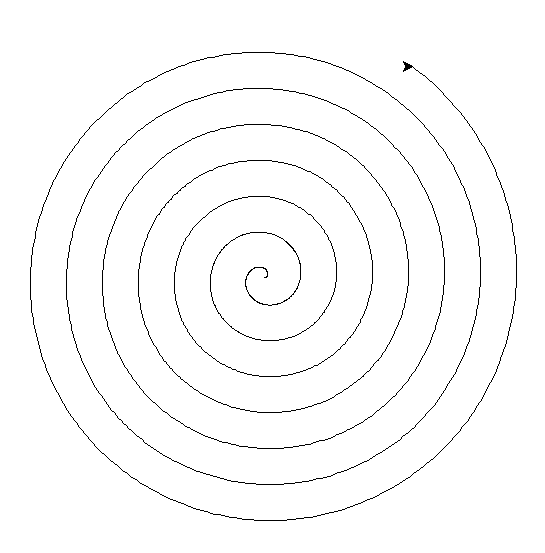 3代码
3代码import turtle import math wn = turtle.Screen() wn.bgcolor=("black") turtle.pencolor=('beige') t = turtle.Turtle() a = 0.1 for theta in range(10086): r = a * theta x = r * math.cos(math.radians(theta)) y = r * math.sin(math.radians(theta)) t.goto(x, y) t.hideturtle()4原理
 👍 5👎 4
👍 5👎 4 -
 @ 2024-11-10 16:20:12
@ 2024-11-10 16:20:12- 每个基本图形是一个等边三角形,边长为300 重复36次,每次绘制一个等边三角形每次绘制一个三角形后,画笔右转10度
2.
 3.
3.import turtle as t def draw_s(t, size): for _ in range(4): t.forward(size) t.right(120)#画三角形 def d_p(t,n_s,size,angle): for _ in range(n_s): draw_s(t, size) t.right(angle)#重复画三角形 t.color("green") t.speed(0) t.pensize(3) n_s=36 size=300 angle=10 d_p(t,n_s,size,angle) t.done()👎 2 -
@ 2024-11-10 16:18:28
1.设计与思考
仿照角度变换的四边形,旋转变化
2.作品图片


3.代码
import turtle as t y=6 x=5 t.pensize(5) t.setup(width=1000,height=1000) t.bgcolor("black") colors = ["red", "purple", "yellow", "blue"] t.speed(0) while x < 500: t.pencolor(colors[x % 4]) for _ in range(y): t.forward(x) t.left(51) x = x + 5 t.done()😄 4👍 2👎 2 -
 @ 2024-11-10 16:18:00
@ 2024-11-10 16:18:00用户输入一个自然数n 程序会生成一个0到n的质数列表,并以列表中的元素为边数画出一个递归图案 用来直观看出质数的一些特性 图片
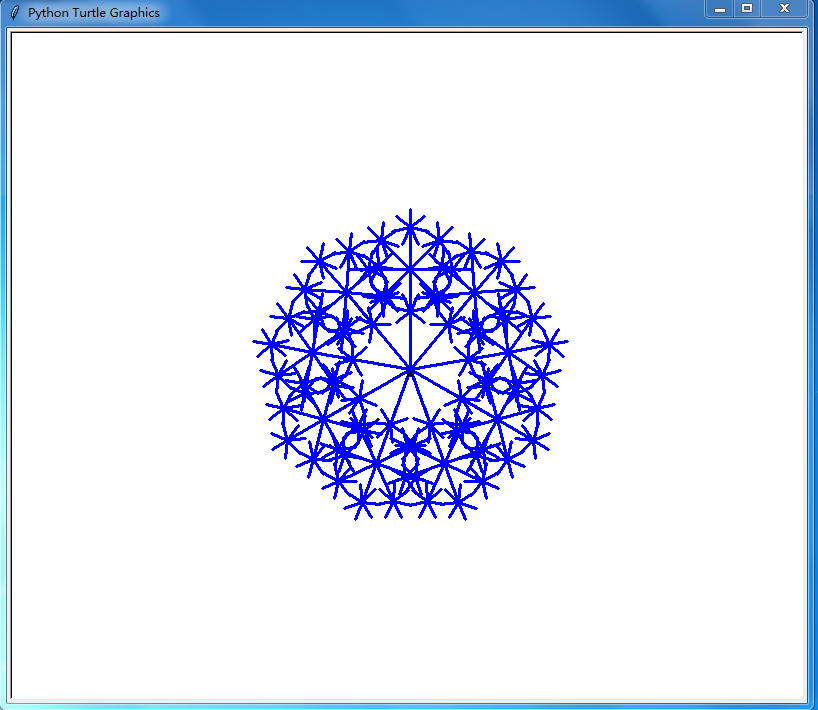
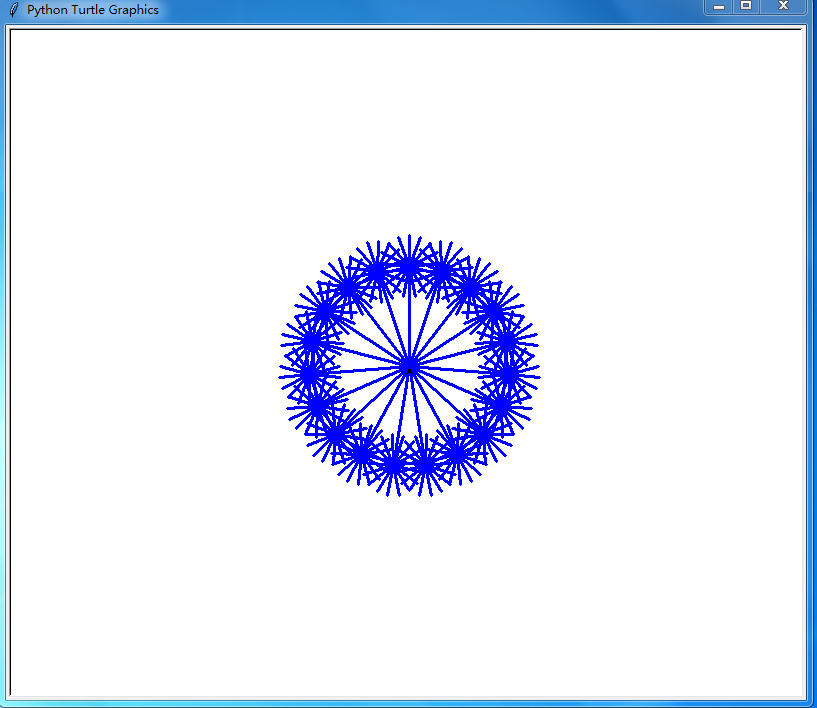
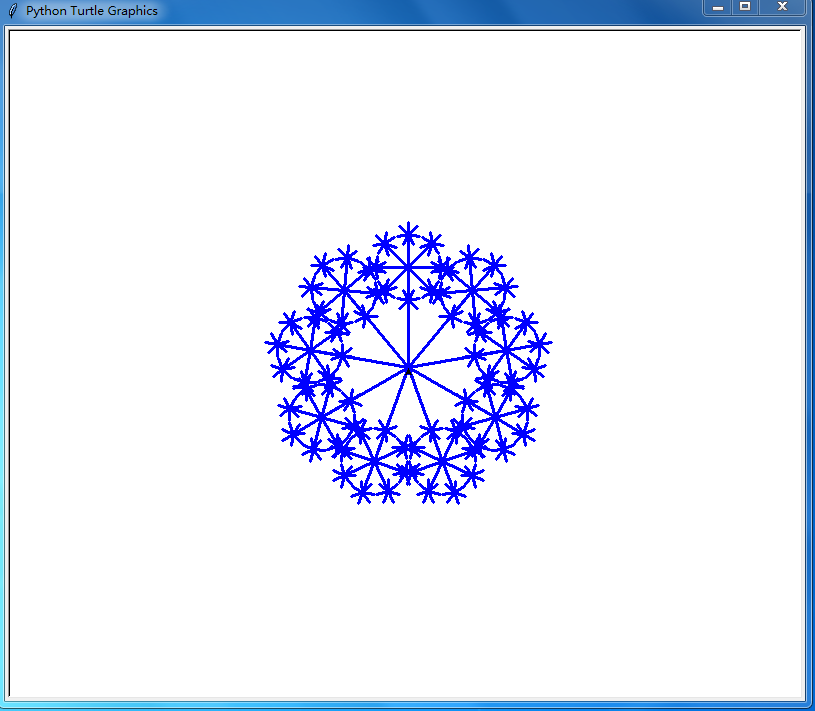
import turtle as p def iszhishu(a): cnt=True for i in range(2,int(a**0.5)): if a%i==0: cnt=False break return cnt def tuxing(n,t): for i in range(number[t]): p.fd(n) if n/(number[t]**0.5)>10: tuxing(n/(number[t]**0.5),t-1) p.bk(n) p.rt(360/number[t]) number=[] x=p.numinput("长度输入","请输入长度,turtle将画出一个美丽的递归图形",100,40,1000) y=p.numinput("自然数n输入","请输入一个自然数,turtle将画出一个以0到n的质数为主要边数的递归图案",10,3,50) y=int(y) x=int(x) for i in range(2,y+1): if iszhishu(i): number.append(i) p.lt(90) p.pencolor("blue") p.pensize(3) p.speed(0) tuxing(int(x),-1)👍 5👎 2 -
 @ 2024-11-10 16:17:07
@ 2024-11-10 16:17:071.图案设计思考: 制作多个个多颜色的六边形,查看RGB颜色分布的排列 2绘制的图案:

import turtle as t t.colormode(255) t.speed(5408) t.pensize(5) m=5 def dr(): for i in range(4): t.fd(m) t.right(60) while m<255: for i in range(1,255,1): for j in range(1,255,1): for k in range(1,255,1): dr() t.pencolor(k,j,i) t.fd(5) m=m+5 t.done()👍 3🕊️ 3👎 2❤️ 1🌿 1👀 1😄 1 -
 @ 2024-11-10 16:16:58
@ 2024-11-10 16:16:58绘制谢尔宾斯基三角形
1. 图案设计思考:
设计绘制的图案由多个三角形构成的
构造
一个实心的等边三角形。沿三边中点的连线,将它分成四个小三角形,去掉中间的那一个小三角形,对其余三个小三角形重复
2. 绘制的图像:
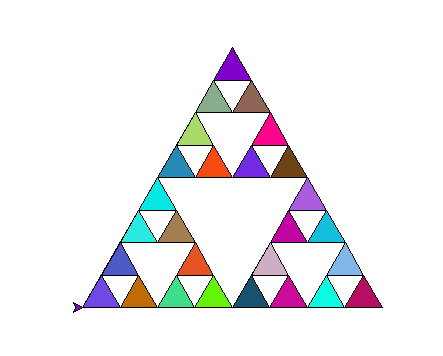
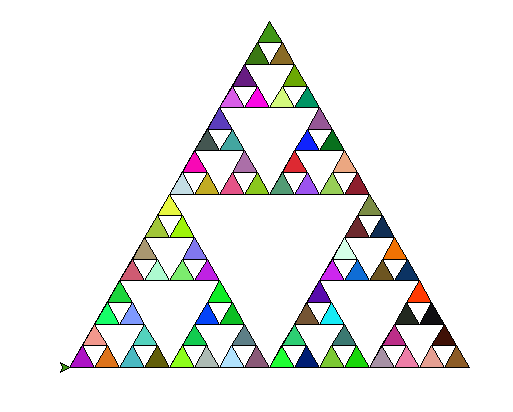
3. 绘制的代码:
import turtle as t import random t.colormode(255) def sierpinski(q1, q2): if q2 == 0: t.begin_fill() # 生成随机255颜色 r = random.randint(0,255) g = random.randint(0,255) b = random.randint(0,255) t.fillcolor((r, g, b)) for _ in range(3): t.fd(q1) t.left(120) t.end_fill() else: sierpinski(q1/2, q2 - 1) t.forward(q1/2) sierpinski(q1/2, q2 - 1) t.backward(q1/2) t.left(60) t.forward(q1/2) t.right(60) sierpinski(q1/2, q2 - 1) t.left(60) t.backward(q1/2) t.right(60) t.speed(0) a1 = int(input('谢尔宾斯基三角形的大小(300~500):')) a2 = int(input('谢尔宾斯基三角形的数量(1~5):')) sierpinski(a1, a2) t.done()👍 6👎 4 -
@ 2024-11-10 16:15:40
import turtle as t t.pencolor("red") t.pensize(5) def px(a,b): t.fd(b) t.forward(b) t.left(90) t.forward(b) t.left(90) t.forward(b) t.left(90) t.forward(b) t.left(90) n=int(input("请输入设计图案的个数:")) a=360/n b=100 for i in range(n): px(a,b) t.left(a) t.done()特征:重复n次,画n个正方形,旋转360/n度
 👎 4😄 4😕 4❤️ 4🤔 4🤡 4👍 3🤣 3🌿 3🍋 3🕊️ 3👀 3
👎 4😄 4😕 4❤️ 4🤔 4🤡 4👍 3🤣 3🌿 3🍋 3🕊️ 3👀 3 -
@ 2024-11-10 16:15:35
输入不同的值可以改变图形的颜色和形状


import turtle as t c=["red","blue","green","yellow","pink","purple","orange","black","grey","silver"] t.pensize(3) a=2 b=int(input("输入的数在1-10中,颜色数量:")) e=b-2 f=e*180 d=f/b+32 t.speed(0) for i in range(100000): t.fd(a) t.pencolor(c[i%b]) t.left(d) a=a+0.5 t.done()👍 4👎 3 -
 @ 2024-11-10 16:14:27
@ 2024-11-10 16:14:271.图案设计思考 用8个颜色画图形,重复90次,把多个不同颜色的圆形叠在一起。 2.截图 (1)自己的图

(2)网上原图

```from random import * from turtle import * pensize(4) tracer(n=20,delay=10) c=['red','orange','yellow','green','cyan','blue','plum','lime'] a=90 for i in range(90): color(c[i%8]) for i in range(a): fd(5) lt(360/a) fd(4) rt(8) done()👍 2👎 2 -
@ 2024-11-10 16:13:24
1:思考:在相同的代码中,绘制的边数与角度不同,最终的图形结果会不会是相同的? 2:图像:
 边数为1
边数为1
 边数为3
边数为3
 边数为10
3:代码:
边数为10
3:代码:import turtle as t x=5 n=int(input('n=')) t.pensize(2) colors = ["purple","yellow","blue","pink"] t.speed(0) while x<100000: t.pencolor(colors[x%4]) t.fd(x) t.left(((n-2)*180/n)+1) x=x+5 t.done()思考结果: 无论边数与角度是否相同,图案最终都为螺旋形
👍 5👎 1 -
@ 2024-11-10 16:11:57
海螺号 图形思考: 如何使图形更显立体感?
图形图案:

import turtle as z a=20 z.speed(0.1) z.pencolor('red') c=0.5 z.fillcolor("brown") for i in range(30): z.circle(a) a=a+5 c=c+0.3 z.left(20) z.pensize(c)👎 2👍 1 -
 @ 2024-11-10 16:11:23
@ 2024-11-10 16:11:231.输入q,r,重复q次绘制角度为r的螺旋线 2.图案样例
 重复5次,以100为初始角度
重复5次,以100为初始角度
 重复5次,以45为初始角度
3.代码
重复5次,以45为初始角度
3.代码import turtle as t def draw(q,r): x=1 t.pensize(0.5) for steps in range(q*10): for c in ('orange','red','orange'): t.speed(0) t.color(c) t.forward(x) t.right(r) x=x+1.1 for step in range(q*10): for c in ('green','blue','green'): t.speed(0) t.color(c) t.forward(x) t.right(r) x=x+1.1 q=int(input("请输入重复次数:")) r=int(input("请输入初始旋转角度(45~179):")) print("waiting....") draw(q,r) print("finish") t.done()👍 3👎 2❤️ 1 -
 @ 2024-11-10 16:09:28
@ 2024-11-10 16:09:28turtle有规律图形创作——王楚墨
1.图案设计思考:让一个三角形和另一个三角形重合,让一个三角形和另两个三角形重合,让一个三角形和 N 个三角形重合,会出现怎样的效果?
2.绘制的图像:

3.绘制的代码:
```from turtle import* pensize(3) bgcolor("#99FFCC") speed(0.01) color1=["#2ECC71","#FFE4B5","#00008B","#00FFFF","#8FBC8F","#36A2EB"] x=1 while True: a=input("run") if a=="Y": n=int(numinput("绘制n个三角形","输入数量(1~500)",1,1,500)) for i in range(n): pencolor(color1[i%6]) backward(x) left(251) x+=2 else: break👍 6👎 1 -
 @ 2024-11-10 16:09:20
@ 2024-11-10 16:09:201.在每次循环中,x 会被增加两次在每次循环中,海龟分别向左转 80 度和 50 度第一次前进距离为当前的 x 值, 第二次前进距离同样为更新后的 x 值 第三次前进固定距离 100(于齐老师的代码增加修改) 2.绘制图形
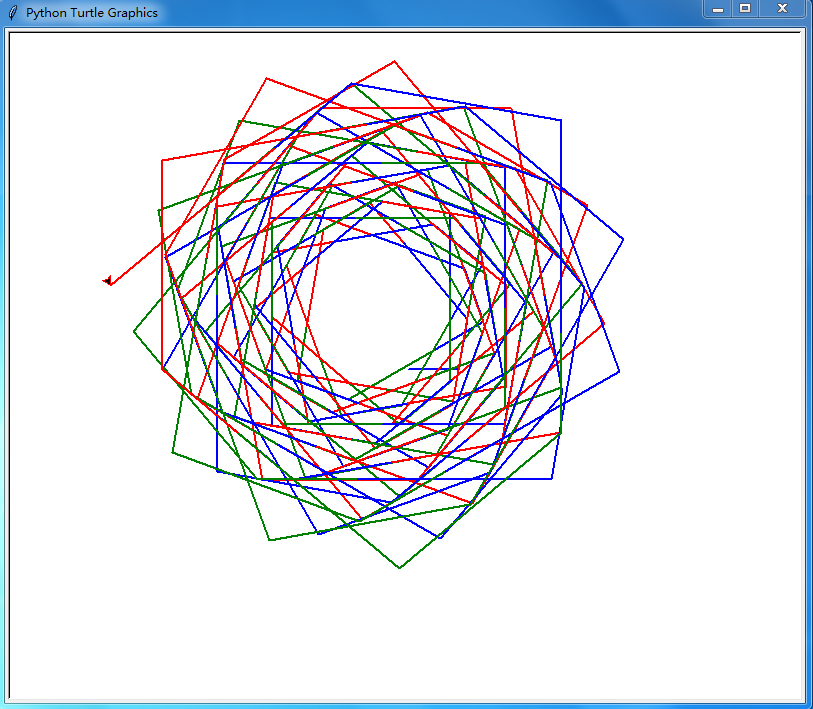 3.绘制代码
3.绘制代码import turtle as t x=50 t.pensize(2) colors = ["green","red","blue"] t.speed(0) while 1: t.pencolor(colors[x%3]) t.forward(x) t.left(80) x=x+1 t.forward(x) t.left(50) x=x+1 t.fd(100) t.done()👍 2 -
 @ 2024-11-10 16:07:42
@ 2024-11-10 16:07:421.(以用户输入的x1,x2,y1,y2)建立一个坐标系,输入数字n,画一个以n*2为半径的圆,旋转n度 2.



from turtle import * x1=int(numinput("建立坐标系", "x1(负数,-100~0)", -50, minval=-100, maxval=0)) x2=int(numinput("建立坐标系", "x2(负数,-100~0,图形按x1:x2为比例)", -50, minval=-100, maxval=0)) y1=int(numinput("建立坐标系", "y1(-x1)", 50, minval=0, maxval=100)) y2=int(numinput("建立坐标系", "y2(-x2)", 50, minval=0, maxval=100)) reset() setworldcoordinates(x1,x2,y1,y2) speed(0) n=int(numinput("图形", "输入(3~15)", 5, minval=3, maxval=15)) i=360/n rt(45) for _ in range(80): circle(n*2) rt(n)👍 6😄 4👎 1 -
 @ 2024-11-10 16:02:28
@ 2024-11-10 16:02:281.设置背景为黑色,输入n,重复绘制n为长度的正方形并重复旋转90度直到中心为圆。 2.长度为80图案:

3.代码:
import turtle turtle.pensize(2) turtle.screensize(bg="black") turtle.pencolor("white") n=int(input('长度n=')) def main(): count = 1 while count <= 144: turtle.forward(n) turtle.right(90) count += 1 if count%4==0: turtle.right(10) if __name__=='__main__': main()👍 3👎 2😄 1 -
 @ 2024-11-10 16:02:18
@ 2024-11-10 16:02:181.该图案是以8种颜色的花瓣组成的花,你可以自己控制花瓣的数量。 2.绘制的图片 (1)网上的原图:
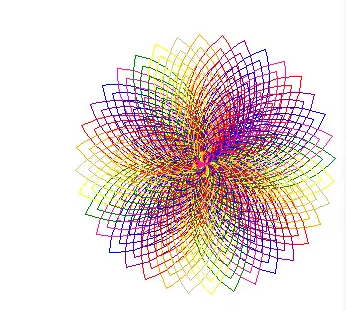
(2)改进后 10片花瓣:

18片花瓣:

3.绘制的代码:
from turtle import * bgcolor("black") tracer(n=20,delay=10) pensize(1) def basehua(m): a=10 c=["red","orange","gold","limegreen","blue","deepskyblue","darkviolet","pink"] for i in range(10): for i in range(m): color(c[i%8]) for i in range(2): for i in range(30): fd(a) lt(3) lt(90) rt(360/m) a=a-1 #实现逻辑框架是网上的,但花瓣的大小,层数,数量,颜色,形状都是我自己改的 n=int(input()) basehua(n) done()👍 18 -
 @ 2024-11-10 15:53:35
@ 2024-11-10 15:53:351.会不断回旋 2.图片

3.代码
#绘制正n角星 import turtle turtle.pensize(10) turtle.speed(0) turtle.screensize(bg="black") a=["lightred","lightorange","lightgold","deepgreen","deepblue","deepskyblue","darkviolet","pink"] turtle.colormode(255) turtle.pencolor('red') n=int(input('n=')) for i in range(n*100): turtle.pencolor(i*i*i%255, i*i%255, i%255) turtle.circle(i,180) if n%2==0: turtle.left( 180-(180-(n-2)*180/n)*2 ) else: turtle.left( (180-(n-2)*180/n)*2 ) turtle.done()👎 8 -
@ 2024-11-10 15:53:17
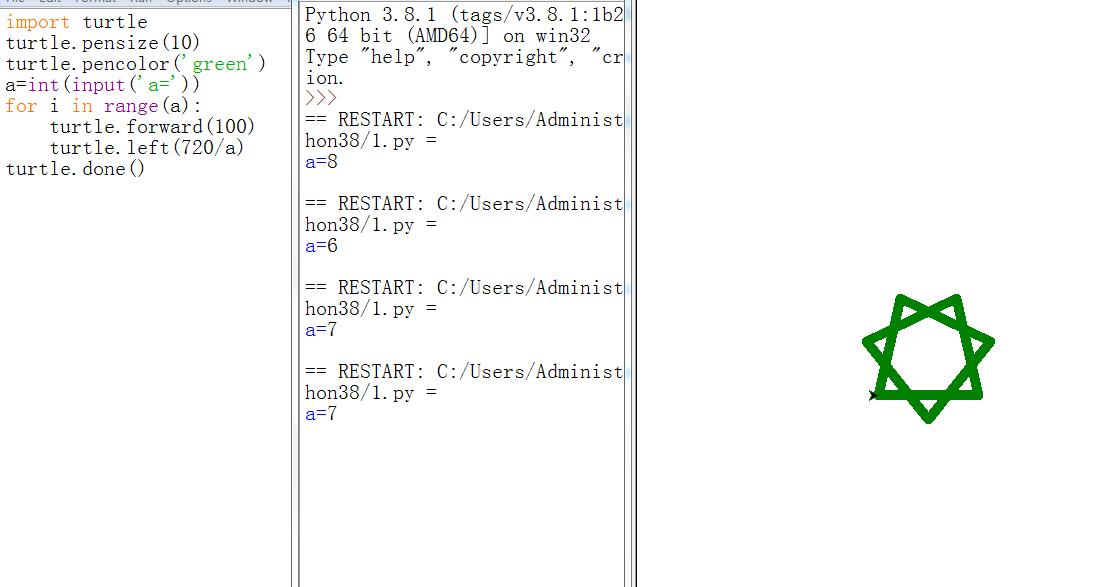
1绘制角度和图形有什么关系 对形状有什么影响
2.绘制的图像:
3.绘制的代码:
import turtle turtle.pensize(10) turtle.pencolor('green') a=int(input('a=')) for i in range(a): turtle.forward(100) turtle.left(720/a) turtle.done()👎 6 -
 @ 2024-11-10 15:52:53
@ 2024-11-10 15:52:53import turtle as t t.speed(0) t.bgcolor("#000000") b=100 a=360/b c=['#BDFCC9','#FFFFFF','#FFC0CB','#F0FFF0','#00FFFF','#F5DEB3'] t.pensize(2) for i in range(b): t.pencolor(c[i%6]) for i in range(2): t.fd(200) t.right(140) t.fd(200) t.right(40) t.left(a)该图以菱形为基础围绕坐标(0.0)为中心旋转所得
 👎 7👍 5
👎 7👍 5 -
 @ 2024-11-10 15:42:26
@ 2024-11-10 15:42:261.图案设计思考:
如何在每个点调用递归?且边长为?何时停止?
2.绘制的图像:
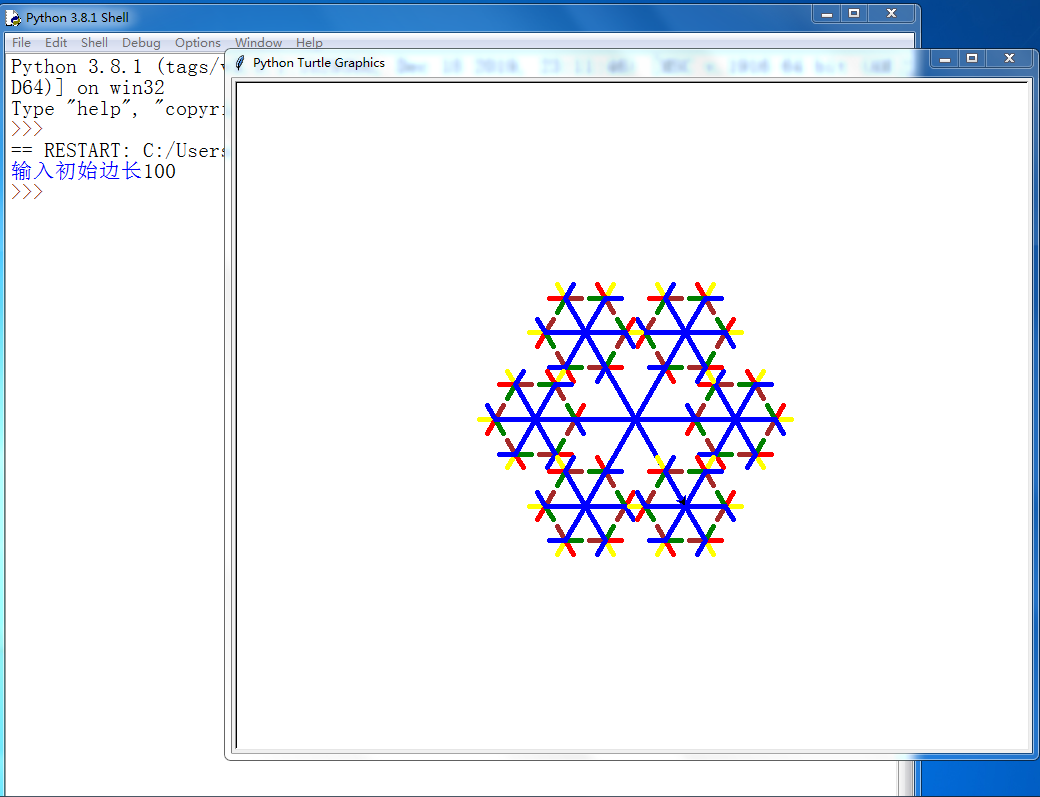
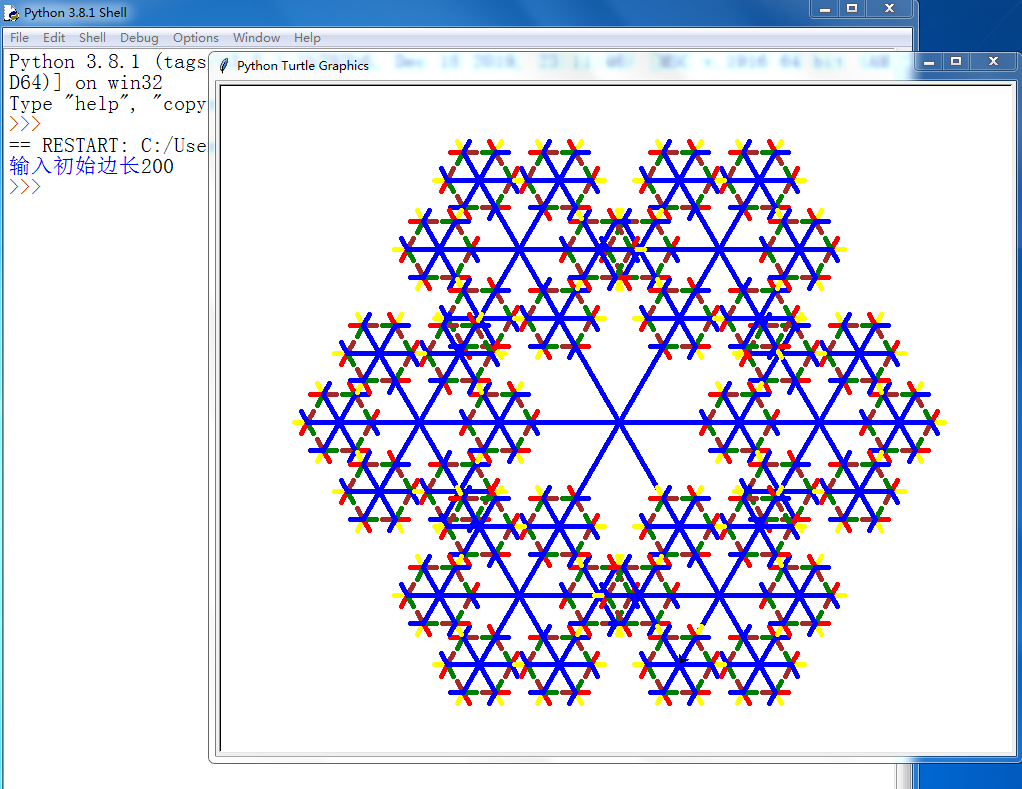
3.绘制的代码:
import turtle as p def a(len): p.pencolor('yellow') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.pencolor('red') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.pencolor('green') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.pencolor('pink') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.pencolor('brown') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.pencolor('blue') p.fd(len) if len*0.4>=10: a(len*0.4) p.bk(len) p.lt(60) p.tracer(n=10, delay=10) p.speed(0) p.pensize(5) p.pencolor('blue') b=int(input('输入初始边长')) a(b)👍 10👎 3 -
@ 2024-11-10 15:42:06
十字 1.图案设计思考:
如何在每个点进行递归 2.绘制的图像:
 3.绘制的代码:
3.绘制的代码:import turtle as p p.speed(0) p.pencolor('blue') p.pensize(5) def f(a): if a<10: return p.fd(a) f(a/2) p.bk(a*2) p.rt(180) f(a/2) p.bk(a) p.lt(90) p.fd(a) f(a/2) p.bk(a*2) p.rt(180) f(a/2) p.bk(a) p.rt(90) h=p.numinput('设置','请输入边长',100,50,300) f(h)👍 8👎 2 -
@ 2024-11-10 11:10:43
绘制星形图形
1.图案设计思考:
设计绘制的图案由n个相同的菱形组成,菱形的一个内角为a,边长为b。在绘制一个菱形的时候:画完一条边,画下一条边之前应该旋转多少度?那么绘制好一个菱形,要绘制下一个菱形时,需要要旋转的角度为?
2.绘制的图像:
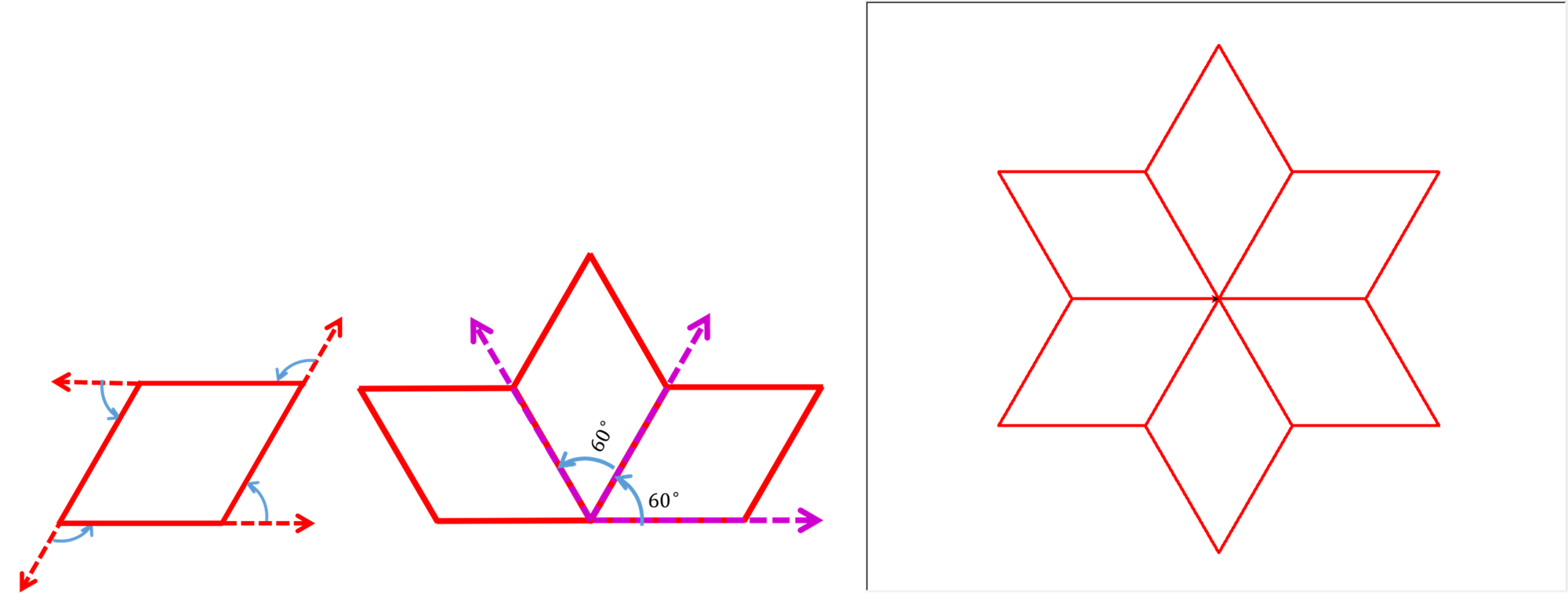
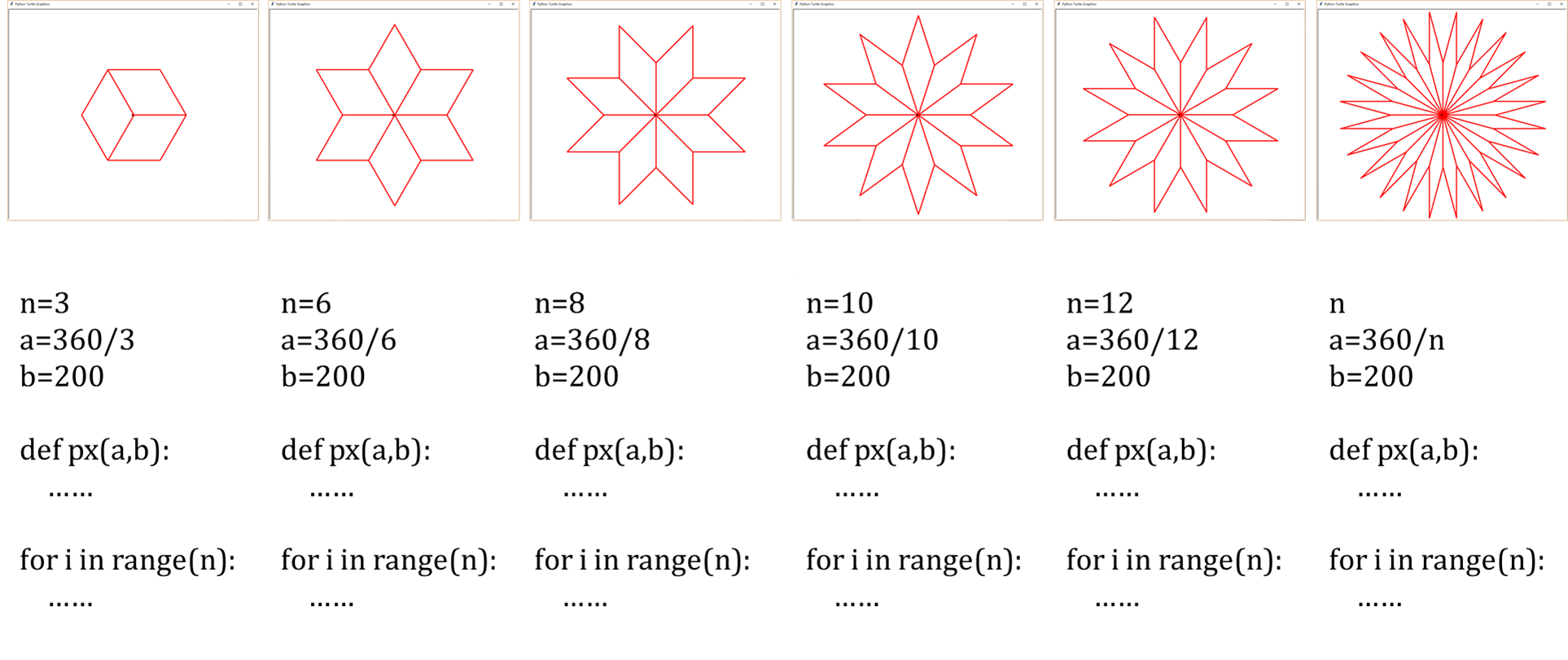
3.绘制的代码:
import turtle as t t.pencolor("red") t.pensize(5) def px(a,b): t.forward(b) t.left(a) t.forward(b) t.left(180-a) t.forward(b) t.left(a) t.forward(b) t.left(180-a) n=int(input("请输入设计图案的菱形个数:")) a=360/n b=100 for i in range(n): px(a,b) t.left(a) t.done()👍 7👎 4 -
@ 2024-11-10 11:07:31
绘制正方形到正n边形,再到绘制螺旋曲线。
1.绘制一个正n边形:
观察正多边形,找到循环次数与边数n之间的关系、旋转角度与边数n之间的关系。
2.尝试绘制多变的螺旋线:
绘制边长变化的图形:在绘制正方形的基础上,边长x初始为5,让它的边长每次循环增加5,边长不超过500,这样多次循环后可以画出如下的图形。运行如下代码,画出变化的图形。
绘制角度变化的图像:每次左转的角度,比如将t.left(91),观察图形发生怎样的变化?如果绘制多彩的旋转图形怎么做。
2.绘制正n边形以及多变螺旋线的图像:
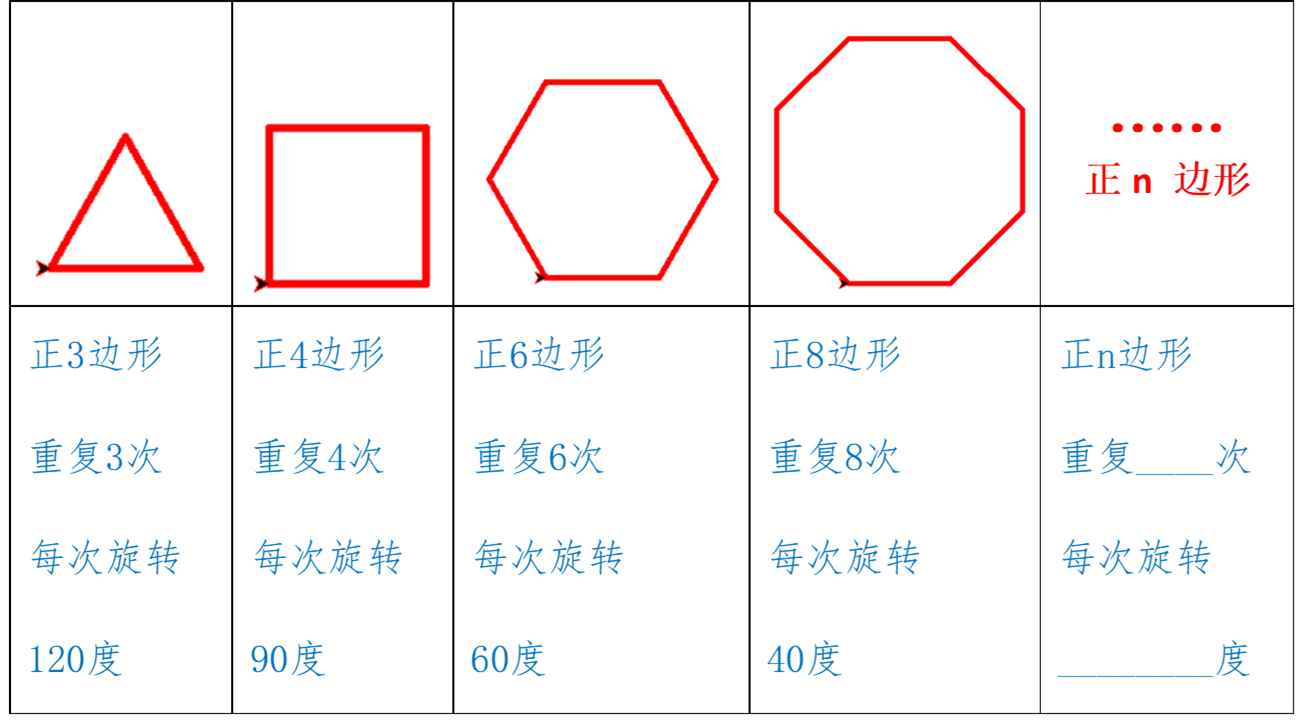
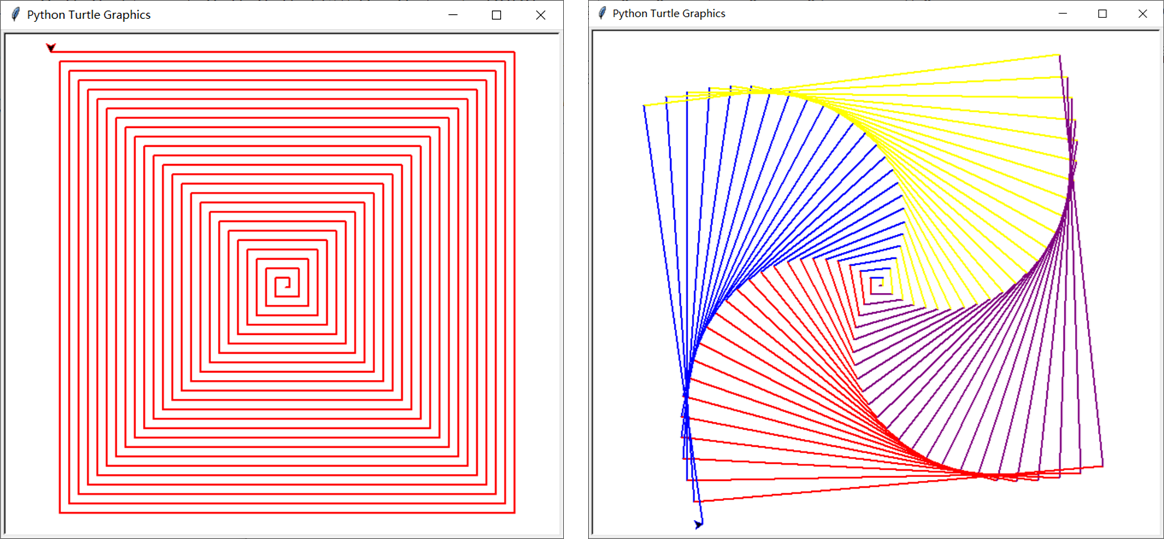
3.绘制的图像代码:
#绘制正n边形 import turtle turtle.pensize(5) turtle.pencolor('red') n=int(input('n=')) for i in range(n): turtle.forward(100) turtle.left(360/n) turtle.done()#绘制边长递增的四边形 import turtle as t x=5 t.pensize(2) t.pencolor("red") while x<500: t.forward(x) t.left(90) x=x+5 t.done()#绘制角度变化的四边形 import turtle as t x=5 t.pensize(2) colors = ["red","purple","yellow","blue"] t.speed(0) while x<500: t.pencolor(colors[x%4]) t.forward(x) t.left(91) x=x+5 t.done()👍 6👎 6😄 5 -
@ 2024-11-10 10:54:16
绘制斐波那契数列图形及曲线
1.f=f1+f2。
斐波那契数列从第3项开始,每一项都等于前两项之和。 (1)输出斐波那契数列;(2)数列转化为图形和曲线;(3)使用颜色列表填充图形;(4)采用RGB数字模式变化地填充图形。
2.绘制斐波那契数列图像截图:

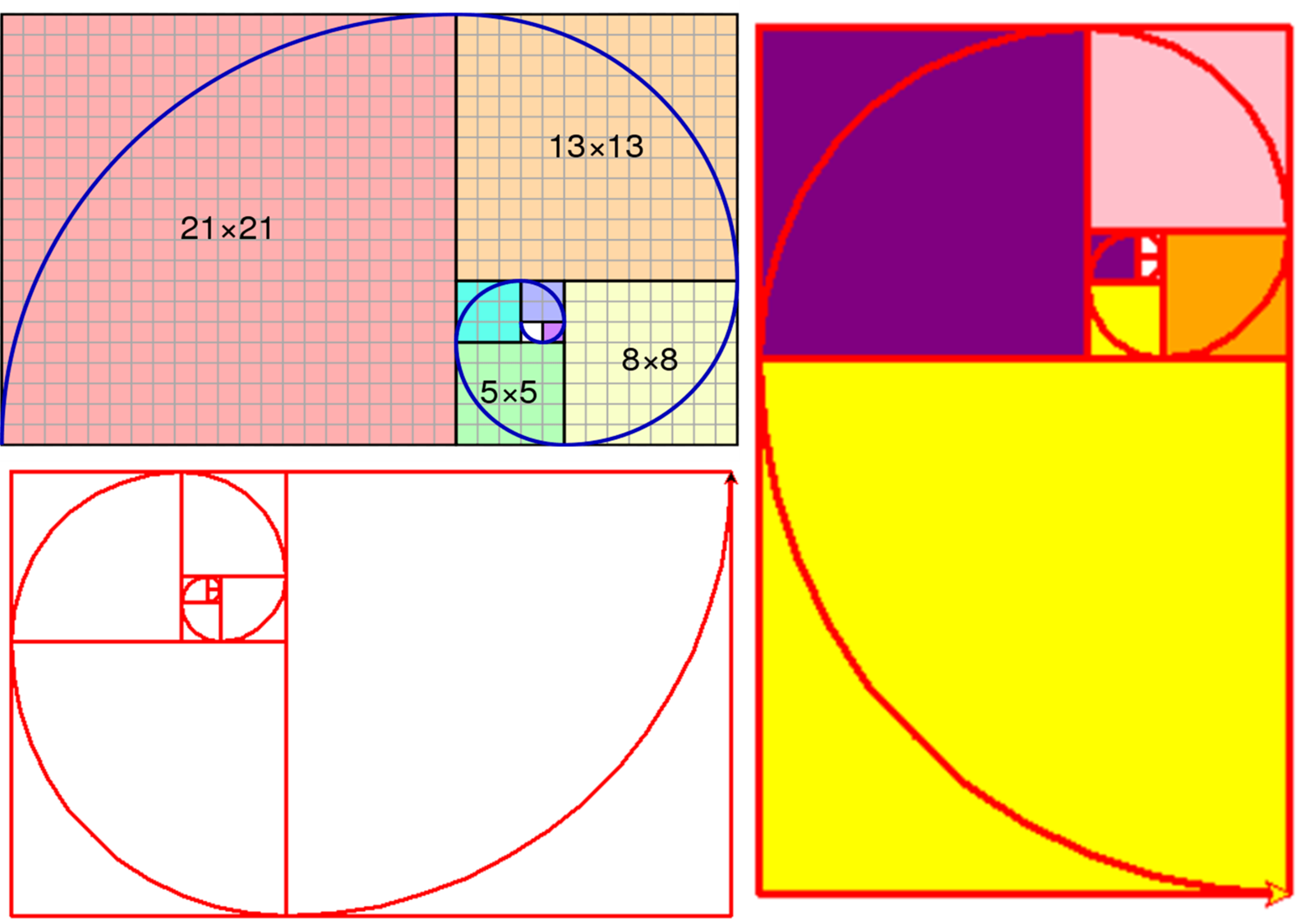
3.绘制斐波那契数列图像代码:
import turtle as t t.pencolor('red') t.pensize(3) def ht(a): t.begin_fill() for i in range(4): t.forward(a*10) t.left(90) t.end_fill() t.circle(a*10,90) n=int(input('项数n(n>2):')) f1=1 f2=1 ht(f1) ht(f2) colors=['yellow','orange','pink','purple'] for i in range(3,n+1): f=f1+f2 t.fillcolor(colors[i%len(colors)]) ht(f) print(f1/f2) f1=f2 f2=f t.done()👎 7👍 6
- 1
